Advertisements
Advertisements
Question
A particle moves on a given straight line with a constant speed ν. At a certain time it is at a point P on its straight line path. O is a fixed point. Show that \[\vec{OP} \times \vec{\nu}\] is independent of the position P.
Solution
The particle moves on the straight line XX' at a uniform speed ν.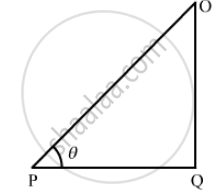
In
\[∆ POQ\]
OQ = OP sin θ
\[\vec{OP} \times \nu = \left( OP \right) \nu \sin \theta \hat n \]
\[ = \nu \left( OP \right) \sin \theta \hat n\]
\[ = \nu\left( OQ \right)\hat n\]
This product is always equal to the perpendicular distance from point O. Also, the direction of this product remains constant.
So, irrespective of the the position of the particle, the magnitude and direction of \[\vec{OP} \times \vec{\nu}\] remain constant. \[\therefore \vec{OP} \times \vec{\nu}\] is independent of the position P.
APPEARS IN
RELATED QUESTIONS
It is often said that the world is witnessing now a second industrial revolution, which will transform the society as radically as did the first. List some key contemporary areas of science and technology, which are responsible for this revolution.
Write in about 100 words a fiction piece based on your speculation on the science and technology of the twenty-second century.
Attempt to formulate your ‘moral’ views on the practice of science. Imagine yourself stumbling upon a discovery, which has great academic interest but is certain to have nothing but dangerous consequences for the human society. How, if at all, will you resolve your dilemma?
Though the law gives women equal status in India, many people hold unscientific views on a woman’s innate nature, capacity and intelligence; and in practice give them a secondary status and role. Demolish this view using scientific arguments, and by quoting examples of great women in science and other spheres; and persuade yourself and others that, given equal opportunity, women are on par with men.
The metre is defined as the distance travelled by light in `1/(299,792,458)` second. Why didn't people choose some easier number such as `1/(300,000,000)` second? Why not 1 second?
Suppose you are told that the linear size of everything in the universe has been doubled overnight. Can you test this statement by measuring sizes with a metre stick? Can you test it by using the fact that the speed of light is a universal constant and has not changed? What will happen if all the clocks in the universe also start running at half the speed?
Suggest a way to measure the distance between the sun and the moon.
Find the dimensions of magnetic dipole moment M.
The defining equations are p = q.d and M = IA;
where d is distance, A is area, q is charge and I is current.
Express the power of a 100 watt bulb in CGS unit.
The kinetic energy K of a rotating body depends on its moment of inertia I and its angular speedω. Assuming the relation to be \[k = KI^0w^B\] where k is a dimensionless constant, find a and b. Moment of inertia of a sphere about its diameter is \[\frac{2}{5}M r^2\]
The force on a charged particle due to electric and magnetic fields is given by \[\vec{F} = q \vec{E} + q \vec{\nu} \times \vec{B}\].
Suppose \[\vec{E}\] is along the X-axis and \[\vec{B}\] along the Y-axis. In what direction and with what minimum speed ν should a positively charged particle be sent so that the net force on it is zero?
The electric current in a discharging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters and t is time. Let i0 = 2⋅00 A, R = 6⋅00 × 105 Ω and C = 0⋅500 μF. (a) Find the current at t = 0⋅3 s. (b) Find the rate of change of current at at 0⋅3 s. (c) Find approximately the current at t = 0⋅31 s.
Find the area bounded under the curve y = 3x2 + 6x + 7 and the X-axis with the ordinates at x = 5 and x = 10.
Find the area enclosed by the curve y = sin x and the X-axis between x = 0 and x = π.
Find the area bounded by the curve y = e−x, the X-axis and the Y-axis.
