Advertisements
Advertisements
Question
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
Advertisements
Solution
Given: \[\vec{A} , \vec{B} \text{ and }\vec{C}\] are mutually perpendicular. \[\vec{A} \times \vec{B}\] is a vector with its direction perpendicular to the plane containing \[\vec{A} \text{ and } \vec{B}\]
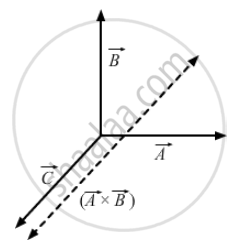
∴ The angle between \[\vec{C} \text{ and } \vec{A} \times \vec{B}\] is either 0° or 180°.
i.e., \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] However, the converse is not true. For example, if two of the vectors are parallel, then also, \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\]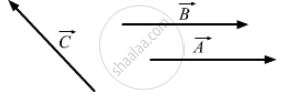 
So, they need not be mutually perpendicular.
APPEARS IN
RELATED QUESTIONS
“Politics is the art of the possible”. Similarly, “Science is the art of the soluble”. Explain this beautiful aphorism on the nature and practice of science.
It is desirable that the standards of units be easily available, invariable, indestructible and easily reproducible. If we use foot of a person as a standard unit of length, which of the above features are present and which are not?
A unitless quantity
Choose the correct statements(s):
(a) All quantities may be represented dimensionally in terms of the base quantities.
(b) A base quantity cannot be represented dimensionally in terms of the rest of the base quantities.
(c) The dimensions of a base quantity in other base quantities is always zero.
(d) The dimension of a derived quantity is never zero in any base quantity.
Find the dimensions of frequency .
Find the dimensions of pressure.
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Find the dimensions of the specific heat capacity c.
(a) the specific heat capacity c,
(b) the coefficient of linear expansion α and
(c) the gas constant R.
Some of the equations involving these quantities are \[Q = mc\left( T_2 - T_1 \right), l_t = l_0 \left[ 1 + \alpha\left( T_2 - T_1 \right) \right]\] and PV = nRT.
The height of mercury column in a barometer in a Calcutta laboratory was recorded to be 75 cm. Calculate this pressure in SI and CGS units using the following data : Specific gravity of mercury = \[13 \cdot 6\] , Density of \[\text{ water} = {10}^3 kg/ m^3 , g = 9 \cdot 8 m/ s^2\] at Calcutta. Pressure
= hpg in usual symbols.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
A vector is not changed if
A vector \[\vec{A}\] points vertically upward and \[\vec{B}\] points towards the north. The vector product \[\vec{A} \times \vec{B}\] is
A situation may be described by using different sets coordinate axes having different orientation. Which the following do not depended on the orientation of the axis?
(a) the value of a scalar
(b) component of a vector
(c) a vector
(d) the magnitude of a vector.
Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that
cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0.
Use the known cosine values to verify the result.
If \[\vec{A} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{B} = 4 \vec{i} + 3 \vec{j} + 2 \vec{k}\] find \[\vec{A} \times \vec{B}\].
