Advertisements
Advertisements
प्रश्न
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
उत्तर
Given: \[\vec{A} , \vec{B} \text{ and }\vec{C}\] are mutually perpendicular. \[\vec{A} \times \vec{B}\] is a vector with its direction perpendicular to the plane containing \[\vec{A} \text{ and } \vec{B}\]
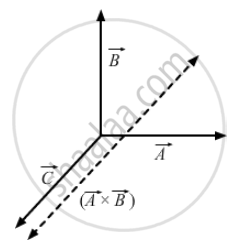
∴ The angle between \[\vec{C} \text{ and } \vec{A} \times \vec{B}\] is either 0° or 180°.
i.e., \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] However, the converse is not true. For example, if two of the vectors are parallel, then also, \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] 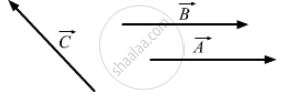
So, they need not be mutually perpendicular.
APPEARS IN
संबंधित प्रश्न
India has had a long and unbroken tradition of great scholarship — in mathematics, astronomy, linguistics, logic and ethics. Yet, in parallel with this, several superstitious and obscurantistic attitudes and practices flourished in our society and unfortunately continue even today — among many educated people too. How will you use your knowledge of science to develop strategies to counter these attitudes ?
What are the dimensions of volume of a cube of edge a.
A physical quantity is measured and the result is expressed as nu where u is the unit used and n is the numerical value. If the result is expressed in various units then
Suppose a quantity x can be dimensionally represented in terms of M, L and T, that is, `[ x ] = M^a L^b T^c`. The quantity mass
\[\int\frac{dx}{\sqrt{2ax - x^2}} = a^n \sin^{- 1} \left[ \frac{x}{a} - 1 \right]\]
The value of n is
The dimensions ML−1 T−2 may correspond to
Choose the correct statements(s):
Choose the correct statements(s):
(a) All quantities may be represented dimensionally in terms of the base quantities.
(b) A base quantity cannot be represented dimensionally in terms of the rest of the base quantities.
(c) The dimensions of a base quantity in other base quantities is always zero.
(d) The dimension of a derived quantity is never zero in any base quantity.
Find the dimensions of linear momentum .
Find the dimensions of frequency .
Find the dimensions of pressure.
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of magnetic permeability \[\mu_0\]
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
If \[\vec{A} \times \vec{B} = 0\] can you say that
(a) \[\vec{A} = \vec{B} ,\]
(b) \[\vec{A} \neq \vec{B}\] ?
Let the angle between two nonzero vectors \[\vec{A}\] and \[\vec{B}\] be 120° and its resultant be \[\vec{C}\].
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
Suppose \[\vec{a}\] is a vector of magnitude 4.5 units due north. What is the vector (a) \[3 \vec{a}\], (b) \[- 4 \vec{a}\] ?
Let \[\vec{a} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j} + 5 \vec{k}\] Find the angle between them.
The changes in a function y and the independent variable x are related as
\[\frac{dy}{dx} = x^2\] . Find y as a function of x.
