Advertisements
Advertisements
Question
The force on a charged particle due to electric and magnetic fields is given by \[\vec{F} = q \vec{E} + q \vec{\nu} \times \vec{B}\].
Suppose \[\vec{E}\] is along the X-axis and \[\vec{B}\] along the Y-axis. In what direction and with what minimum speed ν should a positively charged particle be sent so that the net force on it is zero?
Solution
According to the problem, the net electric and magnetic forces on the particle should be zero. 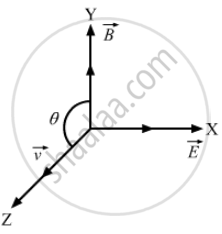
i.e.,
\[\vec{F} = q \vec{E} + q\left( \vec{\nu} \times \vec{B} \right) = 0\]
\[\Rightarrow E = - \left( \vec{\nu} \times \vec{B} \right)\]
So, the direction of \[\vec{\nu} \times \vec{B}\] should be opposite to the direction of \[\vec{E}\] Hence, \[\vec{\nu}\] should be along the positive z-direction.
Again, E = νB sin θ
\[\Rightarrow \nu = \frac{E}{B} \sin \theta\]
For ν to be minimum, \[\theta = 90 \text{ and }, thus, \nu_\min = \frac{E}{B}\]
So, the particle must be projected at a minimum speed of \[\frac{E}{B}\] along the z-axis.
APPEARS IN
RELATED QUESTIONS
It is often said that the world is witnessing now a second industrial revolution, which will transform the society as radically as did the first. List some key contemporary areas of science and technology, which are responsible for this revolution.
Attempt to formulate your ‘moral’ views on the practice of science. Imagine yourself stumbling upon a discovery, which has great academic interest but is certain to have nothing but dangerous consequences for the human society. How, if at all, will you resolve your dilemma?
Science, like any knowledge, can be put to good or bad use, depending on the user.Given below are some of the applications of science. Formulate your views on whether the particular application is good, bad or something that cannot be so clearly categorized :
(a) Mass vaccination against smallpox to curb and finally eradicate this disease from the population. (This has already been successfully done in India.)
(b) Television for the eradication of illiteracy and for mass communication of news and ideas.
(c) Prenatal sex determination.
(d) Computers for the increase in work efficiency.
(e) Putting artificial satellites into orbits around the Earth.
(f) Development of nuclear weapons.
(g) Development of new and powerful techniques of chemical and biological warfare.
(h) Purification of water for drinking.
(i) Plastic surgery.
(j) Cloning.
Though the law gives women equal status in India, many people hold unscientific views on a woman’s innate nature, capacity and intelligence; and in practice give them a secondary status and role. Demolish this view using scientific arguments, and by quoting examples of great women in science and other spheres; and persuade yourself and others that, given equal opportunity, women are on par with men.
The metre is defined as the distance travelled by light in `1/(299,792,458)` second. Why didn't people choose some easier number such as `1/(300,000,000)` second? Why not 1 second?
Suppose you are told that the linear size of everything in the universe has been doubled overnight. Can you test this statement by measuring sizes with a metre stick? Can you test it by using the fact that the speed of light is a universal constant and has not changed? What will happen if all the clocks in the universe also start running at half the speed?
Express the power of a 100 watt bulb in CGS unit.
The kinetic energy K of a rotating body depends on its moment of inertia I and its angular speedω. Assuming the relation to be \[k = KI^0w^B\] where k is a dimensionless constant, find a and b. Moment of inertia of a sphere about its diameter is \[\frac{2}{5}M r^2\]
The electric current in a discharging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters and t is time. Let i0 = 2⋅00 A, R = 6⋅00 × 105 Ω and C = 0⋅500 μF. (a) Find the current at t = 0⋅3 s. (b) Find the rate of change of current at at 0⋅3 s. (c) Find approximately the current at t = 0⋅31 s.
Find the area bounded under the curve y = 3x2 + 6x + 7 and the X-axis with the ordinates at x = 5 and x = 10.
Find the area enclosed by the curve y = sin x and the X-axis between x = 0 and x = π.
A rod of length L is placed along the X-axis between x = 0 and x = L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ = a + bx. (a) Find the SI units of a and b. (b) Find the mass of the rod in terms of a, b and L.
A metre scale is graduated at every millimetre. How many significant digits will be there in a length measurement with this scale?
