Advertisements
Advertisements
Question
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
Advertisements
Solution
To prove:
\[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B,} \text{ but } \vec{A} \neq \vec{C}\]
Suppose that
\[\vec{A}\] is perpendicular to
\[\vec{B};\vec{B}\] is along the west direction.
Also, \[\vec{B}\] is perpendicular to `vecC ; vecA`
\[\vec{C}\] are along the south and north directions, respectively.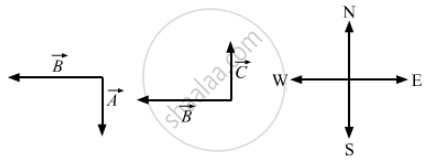
`vecA` is perpendicular to \[\vec{B}\], so there dot or scalar product is zero.
i.e .,
\[\vec{A} \cdot \vec{B} = \left| \vec{A} \right|\left| \vec{B} \right|\cos\theta = \left| \vec{A} \right|\left| \vec{B} \right|\cos90^\circ= 0\]
\[\vec{B}\] is perpendicular to \[\vec{C}\], so there dot or scalar product is zero.
i.e., \[\vec{C} \cdot \vec{B} = \left| \vec{C} \right|\left| \vec{B} \right|cos\theta = \left| \vec{C} \right|\left| \vec{B} \right|cos90\ = 0\]
\[\therefore \vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{C,} but \vec{A} \neq \vec{C}\]
Hence, proved.
APPEARS IN
RELATED QUESTIONS
“Every great physical theory starts as a heresy and ends as a dogma”. Give some examples from the history of science of the validity of this incisive remark
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
A dimensionless quantity
Find the dimensions of linear momentum .
Find the dimensions of frequency .
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
The height of mercury column in a barometer in a Calcutta laboratory was recorded to be 75 cm. Calculate this pressure in SI and CGS units using the following data : Specific gravity of mercury = \[13 \cdot 6\] , Density of \[\text{ water} = {10}^3 kg/ m^3 , g = 9 \cdot 8 m/ s^2\] at Calcutta. Pressure
= hpg in usual symbols.
Test if the following equation is dimensionally correct:
\[v = \frac{1}{2 \pi}\sqrt{\frac{mgl}{I}};\]
where h = height, S = surface tension, \[\rho\] = density, P = pressure, V = volume, \[\eta =\] coefficient of viscosity, v = frequency and I = moment of interia.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Can you add two vectors representing physical quantities having different dimensions? Can you multiply two vectors representing physical quantities having different dimensions?
Let ε1 and ε2 be the angles made by \[\vec{A}\] and -\[\vec{A}\] with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of \[\vec{A}\].
The resultant of \[\vec{A} \text { and } \vec{B}\] makes an angle α with \[\vec{A}\] and β with \[\vec{B}\],
A vector \[\vec{A}\] points vertically upward and \[\vec{B}\] points towards the north. The vector product \[\vec{A} \times \vec{B}\] is
The magnitude of the vector product of two vectors \[\left| \vec{A} \right|\] and \[\left| \vec{B} \right|\] may be
(a) greater than AB
(b) equal to AB
(c) less than AB
(d) equal to zero.
Add vectors \[\vec{A} , \vec{B} \text { and } \vec{C}\] each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
A spy report about a suspected car reads as follows. "The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
Draw a graph from the following data. Draw tangents at x = 2, 4, 6 and 8. Find the slopes of these tangents. Verify that the curve draw is y = 2x2 and the slope of tangent is \[\tan \theta = \frac{dy}{dx} = 4x\]
\[\begin{array}x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ y & 2 & 8 & 18 & 32 & 50 & 72 & 98 & 128 & 162 & 200\end{array}\]
