Advertisements
Advertisements
Question
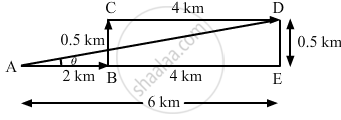
A spy report about a suspected car reads as follows. "The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.
Solution
The displacement of the car is represented by \[\overrightarrow{AD}\].
\[\overrightarrow{AD} = 2 \hat {i}+ 0 . 5 \hat {j} + 4 \hat {i} \]
\[ = 6 \hat {i} + 0 . 5 \hat {j}\]
Magnitude of \[\overrightarrow{AD}\] is given by
\[AD = \sqrt{{AE}^2 + {DE}^2}\]
\[ = \sqrt{6^2 + \left( 0 . 5 \right)^2}\]
\[ = \sqrt{36 + 0 . 25} = 6 . 02 km\]
Now,
\[\tan \theta = \frac{DE}{AE} = \frac{1}{12}\]
\[\Rightarrow \theta = \tan^{- 1} \left( \frac{1}{12} \right)\]
Hence, the displacement of the car is 6.02 km along the direction \[\tan^{- 1} \left( \frac{1}{12} \right)\] with positive the x-axis.
APPEARS IN
RELATED QUESTIONS
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
What are the dimensions of volume of a cube of edge a.
What are the dimensions of the ratio of the volume of a cube of edge a to the volume of a sphere of radius a?
If all the terms in an equation have same units, is it necessary that they have same dimensions? If all the terms in an equation have same dimensions, is it necessary that they have same units?
Suggest a way to measure the thickness of a sheet of paper.
Suppose a quantity x can be dimensionally represented in terms of M, L and T, that is, `[ x ] = M^a L^b T^c`. The quantity mass
A dimensionless quantity
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Find the dimensions of magnetic permeability \[\mu_0\]
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[h = \frac{2S cos\theta}{\text{ prg }},\]
where h = height, S = surface tension, ρ = density, I = moment of interia.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Let \[\vec{C} = \vec{A} + \vec{B}\]
The x-component of the resultant of several vectors
(a) is equal to the sum of the x-components of the vectors of the vectors
(b) may be smaller than the sum of the magnitudes of the vectors
(c) may be greater than the sum of the magnitudes of the vectors
(d) may be equal to the sum of the magnitudes of the vectors.
A vector \[\vec{A}\] makes an angle of 20° and \[\vec{B}\] makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
A carrom board (4 ft × 4 ft square) has the queen at the centre. The queen, hit by the striker moves to the from edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a) from the centre to the front edge, (b) from the front edge to the hole and (c) from the centre to the hole.
The changes in a function y and the independent variable x are related as
\[\frac{dy}{dx} = x^2\] . Find y as a function of x.
Round the following numbers to 2 significant digits.
(a) 3472, (b) 84.16. (c)2.55 and (d) 28.5
In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 s. If the speed of sound in water is 1460 ms-1. What is the distance of an enemy submarine?
