Advertisements
Advertisements
Question
Draw a graph from the following data. Draw tangents at x = 2, 4, 6 and 8. Find the slopes of these tangents. Verify that the curve draw is y = 2x2 and the slope of tangent is \[\tan \theta = \frac{dy}{dx} = 4x\]
\[\begin{array}x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ y & 2 & 8 & 18 & 32 & 50 & 72 & 98 & 128 & 162 & 200\end{array}\]
Solution
Note: Students should draw the graph y = 2x2 on a graph paper for results.
To find a slope at any point, draw a tangent at the point and extend the line to meet the x-axis. Then find tan θ as shown in the figure.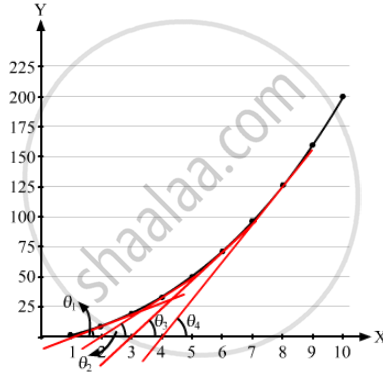
The above can be checked as follows:
\[Slope = \tan \theta = \frac{dy}{dx}\]
\[ = \frac{d}{dx}\left( 2 x^2 \right) = 4x\]
Here, x = x-coordinate of the point where the slope is to be measured.
APPEARS IN
RELATED QUESTIONS
“Politics is the art of the possible”. Similarly, “Science is the art of the soluble”. Explain this beautiful aphorism on the nature and practice of science.
India has had a long and unbroken tradition of great scholarship — in mathematics, astronomy, linguistics, logic and ethics. Yet, in parallel with this, several superstitious and obscurantistic attitudes and practices flourished in our society and unfortunately continue even today — among many educated people too. How will you use your knowledge of science to develop strategies to counter these attitudes ?
What are the dimensions of volume of a sphere of radius a?
A physical quantity is measured and the result is expressed as nu where u is the unit used and n is the numerical value. If the result is expressed in various units then
A unitless quantity
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Theory of relativity reveals that mass can be converted into energy. The energy E so obtained is proportional to certain powers of mass m and the speed c of light. Guess a relation among the quantities using the method of dimensions.
Let I = current through a conductor, R = its resistance and V = potential difference across its ends. According to Ohm's law, product of two of these quantities equals the third. Obtain Ohm's law from dimensional analysis. Dimensional formulae for R and V are \[{\text{ML}}^2 \text{I}^{- 2} \text{T}^{- 3}\] and \[{\text{ML}}^2 \text{T}^{- 3} \text{I}^{- 1}\] respectively.
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Let \[\vec{A} = 3 \vec{i} + 4 \vec{j}\]. Write a vector \[\vec{B}\] such that \[\vec{A} \neq \vec{B}\], but A = B.
Can you have \[\vec{A} \times \vec{B} = \vec{A} \cdot \vec{B}\] with A ≠ 0 and B ≠ 0 ? What if one of the two vectors is zero?
Let the angle between two nonzero vectors \[\vec{A}\] and \[\vec{B}\] be 120° and its resultant be \[\vec{C}\].
Refer to figure (2 − E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of \[\overrightarrow{OA}, \overrightarrow{BC} \text { and } \overrightarrow{DE}\].

Suppose \[\vec{a}\] is a vector of magnitude 4.5 units due north. What is the vector (a) \[3 \vec{a}\], (b) \[- 4 \vec{a}\] ?
Let \[\vec{a} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j} + 5 \vec{k}\] Find the angle between them.
In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 s. If the speed of sound in water is 1460 ms-1. What is the distance of an enemy submarine?
If π = 3.14, then the value of π2 is ______
