Advertisements
Advertisements
Question
If two quantities have same dimensions, do they represent same physical content?
Solution
No, even if two quantities have the same dimensions, they may represent different physical contents.
Example: Torque and energy have the same dimension but represent different physical contents.
APPEARS IN
RELATED QUESTIONS
India has had a long and unbroken tradition of great scholarship — in mathematics, astronomy, linguistics, logic and ethics. Yet, in parallel with this, several superstitious and obscurantistic attitudes and practices flourished in our society and unfortunately continue even today — among many educated people too. How will you use your knowledge of science to develop strategies to counter these attitudes ?
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
What are the dimensions of volume of a cube of edge a.
What are the dimensions of volume of a sphere of radius a?
If all the terms in an equation have same units, is it necessary that they have same dimensions? If all the terms in an equation have same dimensions, is it necessary that they have same units?
Find the dimensions of the specific heat capacity c.
(a) the specific heat capacity c,
(b) the coefficient of linear expansion α and
(c) the gas constant R.
Some of the equations involving these quantities are \[Q = mc\left( T_2 - T_1 \right), l_t = l_0 \left[ 1 + \alpha\left( T_2 - T_1 \right) \right]\] and PV = nRT.
Test if the following equation is dimensionally correct:
\[h = \frac{2S cos\theta}{\text{ prg }},\]
where h = height, S = surface tension, ρ = density, I = moment of interia.
Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
Can a vector have zero component along a line and still have nonzero magnitude?
If \[\vec{A} \times \vec{B} = 0\] can you say that
(a) \[\vec{A} = \vec{B} ,\]
(b) \[\vec{A} \neq \vec{B}\] ?
A vector \[\vec{A}\] points vertically upward and \[\vec{B}\] points towards the north. The vector product \[\vec{A} \times \vec{B}\] is
The x-component of the resultant of several vectors
(a) is equal to the sum of the x-components of the vectors of the vectors
(b) may be smaller than the sum of the magnitudes of the vectors
(c) may be greater than the sum of the magnitudes of the vectors
(d) may be equal to the sum of the magnitudes of the vectors.
Let \[\vec{A} \text { and } \vec{B}\] be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
Let \[\vec{a} = 4 \vec{i} + 3 \vec{j} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j}\]. Find the magnitudes of (a) \[\vec{a}\] , (b) \[\vec{b}\] ,(c) \[\vec{a} + \vec{b} \text { and }\] (d) \[\vec{a} - \vec{b}\].
Two vectors have magnitudes 2 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is (a) 1 unit, (b) 5 unit and (c) 7 unit.
A carrom board (4 ft × 4 ft square) has the queen at the centre. The queen, hit by the striker moves to the from edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a) from the centre to the front edge, (b) from the front edge to the hole and (c) from the centre to the hole.
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
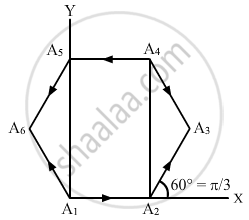
Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that
cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0.
Use the known cosine values to verify the result.
Let \[\vec{a} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j} + 5 \vec{k}\] Find the angle between them.
High speed moving particles are studied under
