Question

Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?

Answer 1

No, it is not possible to obtain zero by adding two vectors of unequal magnitudes.
Example: Let us add two vectors  \[\vec{A}\] and  \[\vec{B}\] of unequal magnitudes acting in opposite directions. The resultant vector is given by 

\[R = \sqrt{A^2 + B^2 + 2AB\cos\theta}\]

If two vectors are exactly opposite to each other, then

\[\theta = 180^\circ, \cos180^\circ= - 1\]

\[R = \sqrt{A^2 + B^2 - 2AB}\]

\[ \Rightarrow R = \sqrt{\left( A - B \right)^2}\]

\[ \Rightarrow R = \left( A - B \right) \text { or } \left( B - A \right)\]

From the above equation, we can say that the resultant vector is zero (R = 0) when the magnitudes of the vectors  \[\vec{A}\] and \[\vec{B}\] are equal (A = B) and both are acting in the opposite directions. 
Yes, it is possible to add three vectors of equal magnitudes and get zero.
Lets take three vectors of equal magnitudes

\[\vec{A,} \vec{B} \text { and } \vec{C}\] ,given these three vectors make an angle of \[120^\circ\] with each other. Consider the figure below:

Lets examine the components of the three vectors.

 

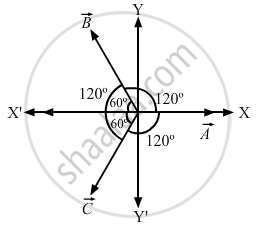
\[A_x = A\]

\[ A_y = 0\]

\[ B_x = - B \cos 60^\circ\]

\[ B_y = B \sin 60^\circ\]

\[ C_x = - C \cos 60^\circ\]

\[ C_y = - C \sin 60^\circ\]

\[\text { Here, A = B = C }\]

So, along the x - axis , we have: 

\[A - (2A \cos 60^\circ) = 0, as \cos 60^\circ = \frac{1}{2} \]

\[ \Rightarrow B \sin 60^\circ - C \sin 60^\circ = 0\]
Hence, proved.