Question

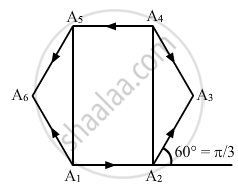
Let A₁ A₂ A₃ A₄ A₅ A₆ A₁ be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that
cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0.
Use the known cosine values to verify the result.

Answer 1

According to the polygon law of vector addition, the resultant of these six vectors is zero.
Here, a = b = c = d = e = f (magnitudes), as it is a regular hexagon. A regular polygon has all sides equal to each other.
So, \[R_x = A \cos 0 + A \cos \frac{\pi}{3} + A \cos \frac{2\pi}{3} + A \cos \frac{3\pi}{3} + A \cos \frac{4\pi}{3} + A \cos \frac{5\pi}{3} = 0\]

[As the resultant is zero, the x-component of resultant R_x is zero]

\[\Rightarrow \cos 0 + \cos \frac{\pi}{3} + \cos \frac{2\pi}{3} + \cos\frac{3\pi}{3} + \cos \frac{4\pi}{3} + \cos \frac{5\pi}{5} = 0\]

Note: Similarly, it can be proven that

\[\sin 0 + \sin \frac{\pi}{3} + \sin \frac{2\pi}{3} + \sin \frac{3\pi}{3} + \sin \frac{4\pi}{3} + \sin \frac{5\pi}{3} = 0\]