Advertisements
Advertisements
प्रश्न
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
उत्तर
To prove:
\[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B,} \text{ but } \vec{A} \neq \vec{C}\]
Suppose that
\[\vec{A}\] is perpendicular to
\[\vec{B};\vec{B}\] is along the west direction.
Also, \[\vec{B}\] is perpendicular to `vecC ; vecA`
\[\vec{C}\] are along the south and north directions, respectively.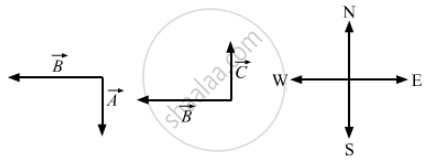
`vecA` is perpendicular to \[\vec{B}\], so there dot or scalar product is zero.
i.e .,
\[\vec{A} \cdot \vec{B} = \left| \vec{A} \right|\left| \vec{B} \right|\cos\theta = \left| \vec{A} \right|\left| \vec{B} \right|\cos90^\circ= 0\]
\[\vec{B}\] is perpendicular to \[\vec{C}\], so there dot or scalar product is zero.
i.e., \[\vec{C} \cdot \vec{B} = \left| \vec{C} \right|\left| \vec{B} \right|cos\theta = \left| \vec{C} \right|\left| \vec{B} \right|cos90\ = 0\]
\[\therefore \vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{C,} but \vec{A} \neq \vec{C}\]
Hence, proved.
APPEARS IN
संबंधित प्रश्न
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
If two quantities have same dimensions, do they represent same physical content?
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Test if the following equation is dimensionally correct:
\[v = \frac{1}{2 \pi}\sqrt{\frac{mgl}{I}};\]
where h = height, S = surface tension, \[\rho\] = density, P = pressure, V = volume, \[\eta =\] coefficient of viscosity, v = frequency and I = moment of interia.
Can you add two vectors representing physical quantities having different dimensions? Can you multiply two vectors representing physical quantities having different dimensions?
A vector is not changed if
Which of the sets given below may represent the magnitudes of three vectors adding to zero?
The resultant of \[\vec{A} \text { and } \vec{B}\] makes an angle α with \[\vec{A}\] and β with \[\vec{B}\],
Let \[\vec{C} = \vec{A} + \vec{B}\]
Let the angle between two nonzero vectors \[\vec{A}\] and \[\vec{B}\] be 120° and its resultant be \[\vec{C}\].
The magnitude of the vector product of two vectors \[\left| \vec{A} \right|\] and \[\left| \vec{B} \right|\] may be
(a) greater than AB
(b) equal to AB
(c) less than AB
(d) equal to zero.
Let \[\vec{A} \text { and } \vec{B}\] be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
Prove that \[\vec{A} . \left( \vec{A} \times \vec{B} \right) = 0\].
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
The electric current in a charging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters of the circuit and t is time. Find the rate of change of current at (a) t = 0, (b) t = RC, (c) t = 10 RC.
Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
