Advertisements
Advertisements
प्रश्न
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
उत्तर
\[V = \frac{\left( \pi P r^4 t \right)}{\left( 8 \eta l \right)}\]
Volume, [V] = [L3]
Pressure,
\[P = \frac{\left[ F \right]}{\left[ A \right]} = \left[ {ML}^{- 1} T^{- 2} \right]\]
[r]= [L] and [t] = [T]
Coefficient of viscosity,
\[\left[ \eta \right] = \frac{\left[ F \right]}{6\pi\left[ r \right]\left[ v \right]} = \frac{\left[ {MLT}^{- 2} \right]}{\left[ L \right]\left[ {LT}^{- 1} \right]} = \left[ {ML}^{- 1} T^{- 1} \right]\]
Now,
\[\frac{\pi\left[ P \right] \left[ r \right]^4 \left[ t \right]}{8\left[ \eta \right]\left[ l \right]} = \frac{\left[ {ML}^{- 1} T^{- 2} \right] \left[ L^4 \right] \left[ T \right]}{\left[ {ML}^{- 1} T^{- 1} \right] \left[ L \right]} = \left[ L^3 \right]\]
Since the dimensions of both sides of the equation are the same, the equation is dimensionally correct.
APPEARS IN
संबंधित प्रश्न
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
What are the dimensions of the ratio of the volume of a cube of edge a to the volume of a sphere of radius a?
If two quantities have same dimensions, do they represent same physical content?
A dimensionless quantity
Find the dimensions of linear momentum .
The height of mercury column in a barometer in a Calcutta laboratory was recorded to be 75 cm. Calculate this pressure in SI and CGS units using the following data : Specific gravity of mercury = \[13 \cdot 6\] , Density of \[\text{ water} = {10}^3 kg/ m^3 , g = 9 \cdot 8 m/ s^2\] at Calcutta. Pressure
= hpg in usual symbols.
Can you add two vectors representing physical quantities having different dimensions? Can you multiply two vectors representing physical quantities having different dimensions?
Can a vector have zero component along a line and still have nonzero magnitude?
Let \[\vec{A} = 5 \vec{i} - 4 \vec{j} \text { and } \vec{B} = - 7 \cdot 5 \vec{i} + 6 \vec{j}\]. Do we have \[\vec{B} = k \vec{A}\] ? Can we say \[\frac{\vec{B}}{\vec{A}}\] = k ?
The resultant of \[\vec{A} \text { and } \vec{B}\] makes an angle α with \[\vec{A}\] and β with \[\vec{B}\],
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
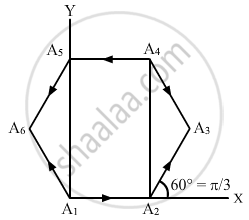
Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that
cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0.
Use the known cosine values to verify the result.
Prove that \[\vec{A} . \left( \vec{A} \times \vec{B} \right) = 0\].
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
A curve is represented by y = sin x. If x is changed from \[\frac{\pi}{3}\text{ to }\frac{\pi}{3} + \frac{\pi}{100}\] , find approximately the change in y.
The changes in a function y and the independent variable x are related as
\[\frac{dy}{dx} = x^2\] . Find y as a function of x.
Jupiter is at a distance of 824.7 million km from the Earth. Its angular diameter is measured to be 35.72˝. Calculate the diameter of Jupiter.
High speed moving particles are studied under
