Advertisements
Advertisements
प्रश्न
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
Advertisements
उत्तर
To prove:
\[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B,} \text{ but } \vec{A} \neq \vec{C}\]
Suppose that
\[\vec{A}\] is perpendicular to
\[\vec{B};\vec{B}\] is along the west direction.
Also, \[\vec{B}\] is perpendicular to `vecC ; vecA`
\[\vec{C}\] are along the south and north directions, respectively.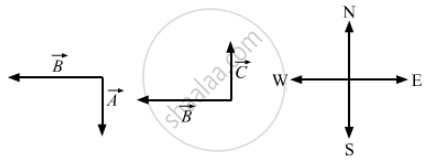
`vecA` is perpendicular to \[\vec{B}\], so there dot or scalar product is zero.
i.e .,
\[\vec{A} \cdot \vec{B} = \left| \vec{A} \right|\left| \vec{B} \right|\cos\theta = \left| \vec{A} \right|\left| \vec{B} \right|\cos90^\circ= 0\]
\[\vec{B}\] is perpendicular to \[\vec{C}\], so there dot or scalar product is zero.
i.e., \[\vec{C} \cdot \vec{B} = \left| \vec{C} \right|\left| \vec{B} \right|cos\theta = \left| \vec{C} \right|\left| \vec{B} \right|cos90\ = 0\]
\[\therefore \vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{C,} but \vec{A} \neq \vec{C}\]
Hence, proved.
APPEARS IN
संबंधित प्रश्न
What are the dimensions of volume of a sphere of radius a?
A unitless quantity
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of Planck's constant h from the equation E = hv where E is the energy and v is the frequency.
Find the dimensions of the specific heat capacity c.
(a) the specific heat capacity c,
(b) the coefficient of linear expansion α and
(c) the gas constant R.
Some of the equations involving these quantities are \[Q = mc\left( T_2 - T_1 \right), l_t = l_0 \left[ 1 + \alpha\left( T_2 - T_1 \right) \right]\] and PV = nRT.
The height of mercury column in a barometer in a Calcutta laboratory was recorded to be 75 cm. Calculate this pressure in SI and CGS units using the following data : Specific gravity of mercury = \[13 \cdot 6\] , Density of \[\text{ water} = {10}^3 kg/ m^3 , g = 9 \cdot 8 m/ s^2\] at Calcutta. Pressure
= hpg in usual symbols.
Test if the following equation is dimensionally correct:
\[h = \frac{2S cos\theta}{\text{ prg }},\]
where h = height, S = surface tension, ρ = density, I = moment of interia.
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Can a vector have zero component along a line and still have nonzero magnitude?
Is the vector sum of the unit vectors \[\vec{i}\] and \[\vec{i}\] a unit vector? If no, can you multiply this sum by a scalar number to get a unit vector?
The resultant of \[\vec{A} \text { and } \vec{B}\] makes an angle α with \[\vec{A}\] and β with \[\vec{B}\],
A vector \[\vec{A}\] makes an angle of 20° and \[\vec{B}\] makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
Add vectors \[\vec{A} , \vec{B} \text { and } \vec{C}\] each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
Let \[\vec{a} = 4 \vec{i} + 3 \vec{j} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j}\]. Find the magnitudes of (a) \[\vec{a}\] , (b) \[\vec{b}\] ,(c) \[\vec{a} + \vec{b} \text { and }\] (d) \[\vec{a} - \vec{b}\].
A spy report about a suspected car reads as follows. "The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.
Prove that \[\vec{A} . \left( \vec{A} \times \vec{B} \right) = 0\].
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
Round the following numbers to 2 significant digits.
(a) 3472, (b) 84.16. (c)2.55 and (d) 28.5
In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 s. If the speed of sound in water is 1460 ms-1. What is the distance of an enemy submarine?
Jupiter is at a distance of 824.7 million km from the Earth. Its angular diameter is measured to be 35.72˝. Calculate the diameter of Jupiter.
