Advertisements
Advertisements
प्रश्न
A vector \[\vec{A}\] points vertically upward and \[\vec{B}\] points towards the north. The vector product \[\vec{A} \times \vec{B}\] is
पर्याय
along the west
along the east
zero
vertically downward.
उत्तर
along the west
The vector product \[\vec{A} \times \vec{B}\] will point towards the west. We can determine this direction using the right hand thumb rule.
APPEARS IN
संबंधित प्रश्न
What are the dimensions of volume of a cube of edge a.
If two quantities have same dimensions, do they represent same physical content?
Find the dimensions of linear momentum .
Find the dimensions of frequency .
Find the dimensions of
(a) angular speed ω,
(b) angular acceleration α,
(c) torque τ and
(d) moment of interia I.
Some of the equations involving these quantities are \[\omega = \frac{\theta_2 - \theta_1}{t_2 - t_1}, \alpha = \frac{\omega_2 - \omega_1}{t_2 - t_1}, \tau = F . r \text{ and }I = m r^2\].
The symbols have standard meanings.
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Find the dimensions of magnetic permeability \[\mu_0\]
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Theory of relativity reveals that mass can be converted into energy. The energy E so obtained is proportional to certain powers of mass m and the speed c of light. Guess a relation among the quantities using the method of dimensions.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Is a vector necessarily changed if it is rotated through an angle?
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Can you have \[\vec{A} \times \vec{B} = \vec{A} \cdot \vec{B}\] with A ≠ 0 and B ≠ 0 ? What if one of the two vectors is zero?
A situation may be described by using different sets coordinate axes having different orientation. Which the following do not depended on the orientation of the axis?
(a) the value of a scalar
(b) component of a vector
(c) a vector
(d) the magnitude of a vector.
Let \[\vec{A} \text { and } \vec{B}\] be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
Let \[\vec{a} = 4 \vec{i} + 3 \vec{j} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j}\]. Find the magnitudes of (a) \[\vec{a}\] , (b) \[\vec{b}\] ,(c) \[\vec{a} + \vec{b} \text { and }\] (d) \[\vec{a} - \vec{b}\].
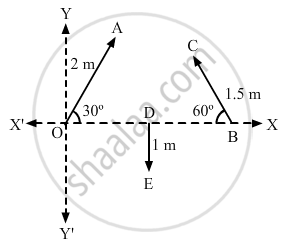
Refer to figure (2 − E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of \[\overrightarrow{OA}, \overrightarrow{BC} \text { and } \overrightarrow{DE}\].
Two vectors have magnitudes 2 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is (a) 1 unit, (b) 5 unit and (c) 7 unit.
A spy report about a suspected car reads as follows. "The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.
Suppose \[\vec{a}\] is a vector of magnitude 4.5 units due north. What is the vector (a) \[3 \vec{a}\], (b) \[- 4 \vec{a}\] ?
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
