Advertisements
Advertisements
प्रश्न
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
उत्तर
Electric field is defined as electric force per unit charge.
i.e., \[E = \frac{F}{q}\]
\[\text{ Also,} \left[ F \right] = {\left[ {MLT}^{- 2} \right]} \text{ and } \left[ q \right] ={\left[ AT \right]}\]
\[\text{ So, dimension of electric field }, [E] = \left[ {MLT}^{- 3} A^{- 1} \right]\]
APPEARS IN
संबंधित प्रश्न
“Every great physical theory starts as a heresy and ends as a dogma”. Give some examples from the history of science of the validity of this incisive remark
\[\int\frac{dx}{\sqrt{2ax - x^2}} = a^n \sin^{- 1} \left[ \frac{x}{a} - 1 \right]\]
The value of n is
Find the dimensions of linear momentum .
Find the dimensions of pressure.
Find the dimensions of magnetic field B.
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Is the vector sum of the unit vectors \[\vec{i}\] and \[\vec{i}\] a unit vector? If no, can you multiply this sum by a scalar number to get a unit vector?
Let \[\vec{A} = 5 \vec{i} - 4 \vec{j} \text { and } \vec{B} = - 7 \cdot 5 \vec{i} + 6 \vec{j}\]. Do we have \[\vec{B} = k \vec{A}\] ? Can we say \[\frac{\vec{B}}{\vec{A}}\] = k ?
A vector \[\vec{A}\] points vertically upward and \[\vec{B}\] points towards the north. The vector product \[\vec{A} \times \vec{B}\] is
A vector \[\vec{A}\] makes an angle of 20° and \[\vec{B}\] makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
Add vectors \[\vec{A} , \vec{B} \text { and } \vec{C}\] each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
Two vectors have magnitudes 2 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is (a) 1 unit, (b) 5 unit and (c) 7 unit.
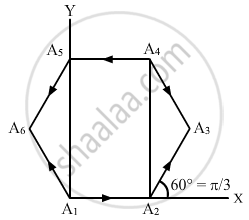
Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that
cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0.
Use the known cosine values to verify the result.
Let \[\vec{a} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j} + 5 \vec{k}\] Find the angle between them.
Prove that \[\vec{A} . \left( \vec{A} \times \vec{B} \right) = 0\].
The electric current in a charging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters of the circuit and t is time. Find the rate of change of current at (a) t = 0, (b) t = RC, (c) t = 10 RC.
Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
Round the following numbers to 2 significant digits.
(a) 3472, (b) 84.16. (c)2.55 and (d) 28.5
