Advertisements
Advertisements
Question
A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametrically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?
Solution
Let “R” be the required location of the pole
Let the distance from the gate P is “x” m : PR = “x” m
The distance from the gate Q is (x + 4)m
∴ QR = (x + 4)m
In the right ∆PQR,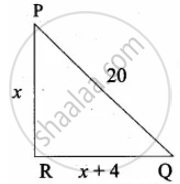
PR2 + QR2 = PQ2 (By Pythagoras theorem)
x2 + (x + 4)2 = 202
x2 + x2 + 16 + 8x = 400
2x2 + 8x – 384 = 0
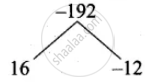
x2 + 4x – 192 = 0 ...(divided by 2)
(x + 16) (x – 12) = 0
x + 16 = 0 or x – 12 = 0 ...[negative value is not considered]
x = – 16 or x = 12
Yes it is possible to erect
The distance from the two gates are 12 m and 16 m
APPEARS IN
RELATED QUESTIONS
Determine the quadratic equation, whose sum and product of roots are `(-3)/2`, – 1
Find the sum and product of the roots for the following quadratic equation
x2 + 3x = 0
Solve the following quadratic equation by factorization method
`sqrt("a"("a" - 7)) = 3sqrt(2)`
Solve the following quadratic equation by completing the square method
`(5x + 7)/(x - 1)` = 3x + 2
A ball rolls down a slope and travels a distance d = t2 – 0.75t feet in t seconds. Find the time when the distance travelled by the ball is 11.25 feet
If the difference between a number and its reciprocal is `24/5`, find the number
A garden measuring 12m by 16m is to have a pedestrian pathway that is ‘ω’ meters wide installed all the way around so that it increases the total area to 285 m2. What is the width of the pathway?
Determine the nature of the roots for the following quadratic equation
`9y^2 - 6sqrt(2)y + 2` = 0
If one root of the equation 2y2 – ay + 64 = 0 is twice the other then find the values of a
If one root of the equation 3x2 + kx + 81 = 0 (having real roots) is the square of the other then find k
