Question

A rectangular tank 30 cm × 20 cm × 12 cm contains water to a depth of 6 cm. A metal cube of side 10 cm is placed in the tank with its one face resting on the bottom of the tank. Find the volume of water, in liters, that must be poured in the tank so that the metal cube is just submerged in the water. 

Answer 1

The dimensions of rectangular tank : 30 cm x 20 cm x 12 cm
Side of the cube = 10 cm
Volume of the Cube = 10³  = 1000 cm³
The height of the water in the tank is 6 cm.
Volume of the cube till 6 cm = 10 x 10 x 6 cm³
Hence when the cube is placed in the tank,
then the volume of the water increases by 600 cm³.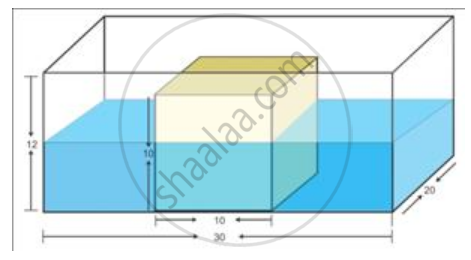

The surface area of the water level is 30 cm x 20 cm = 600 cm²

out of this area, let us subtract the surface area of the cube.

Thus, the surface area of the Shaded part in the above figure is 500 cm²
The displaced water is spread out in 500 cm² to a height of 'h' cm.
And hence the volume of the water.
Thus, we have,
500 x h = 600 cm³
⇒ ` "h" = ( 600/500 )"cm"`
⇒ h = 1.2 cm

Thus, now the level of the water in the tank is = 6 + 1 . 2 = 7 . 2 cm

Remaining height of the water level,
So that the metal cube is just submerged in the water = 100 - 7 . 2 = 2 .8 cm
Thus the volume of the water that must be poured in the tank so that the metal cube is just submerged in the water = 2.8 x 500 = 1400 cm³

We know that 1000 cc = 1 liter

Thus, the required volume of water = ` ( 1400 )/ (1000 )` = 1.4 litres