Advertisements
Advertisements
Question
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
Solution 1
The tension force acting on each wire is the same. Thus, the extension in each case is the same. Since the wires are of the same length, the strain will also be the same.
The relation for Young’s modulus is given as:
`Y = "Stress"/"Strain" = (F/A)/"Strain" = ((4F)/(pid^2))/"Strain"` .....(i)
Where,
F = Tension force
A = Area of cross-section
d = Diameter of the wire
It can be inferred from equation (i) that `Y prop 1/d^2`
Young’s modulus for iron, Y1 = 190 × 109 Pa
Diameter of the iron wire = d1
Young’s modulus for copper, Y2 = 120 × 109 Pa
Diameter of the copper wire = d2
Therefore, the ratio of their diameters is given as:
`d_2/d_1 = sqrt(Y_1/Y_2) = sqrt((190xx10^9)/(120xx10^9)) = sqrt(19/12) = 1:25:1`
Solution 2
Since each wire is to have same tension, therefore, each wire has the same extension. Moreover, each wire has the same initial length.So, the strain is same for each wire.
Now, `Y = "Stress"/"Strain" = (F/((piD^2)/4))/"Strain"`
or `Y prop 1/D^2 => D prop 1/sqrtY`
`D_"copper"/(D_"iron") = sqrt((Y_""iron)/(Y_"copper")) = sqrt((190 xx 10^9)/(110 xx 10^9)) = sqrt(19/11) =1.314`
APPEARS IN
RELATED QUESTIONS
When a block a mass M is suspended by a long wire of length L, the elastic potential potential energy stored in the wire is `1/2` × stress × strain × volume. Show that it is equal to `1/2` Mgl, where l is the extension. The loss in gravitational potential energy of the mass earth system is Mgl. Where does the remaining `1/2` Mgl energy go ?
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
When a metal wire is stretched by a load, the fractional change in its volume ∆V/V is proportional to
A charged particle is moving in a uniform magnetic field in a circular path of radius R. When the energy of the particle becomes three times the original, the new radius will be ______.
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) | 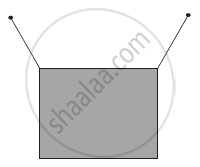 |
| (b) |  |
| (c) | 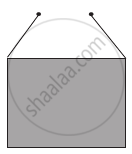 |
The tension in the strings will be ______.
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 × 109 Nm−2 and Ysteel = 200 × 109 Nm–2)
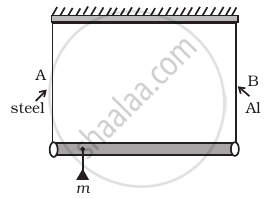
- Mass m should be suspended close to wire A to have equal stresses in both the wires.
- Mass m should be suspended close to B to have equal stresses in both the wires.
- Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
- Mass m should be suspended close to wire A to have equal strain in both wires.
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1πms-2, what will be the tensile stress that would be developed in the wire?
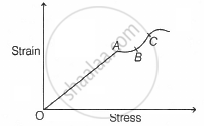
The stress-strain graph of a material is shown in the figure. The region in which the material is elastic is ______.