Advertisements
Advertisements
Question
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 × 109 Nm−2 and Ysteel = 200 × 109 Nm–2)
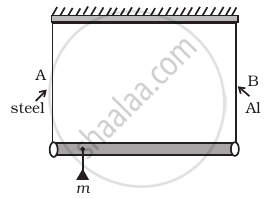
- Mass m should be suspended close to wire A to have equal stresses in both the wires.
- Mass m should be suspended close to B to have equal stresses in both the wires.
- Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
- Mass m should be suspended close to wire A to have equal strain in both wires.
Advertisements
Solution
b and d
Explanation:
Let the mass is placed at x from the end B.
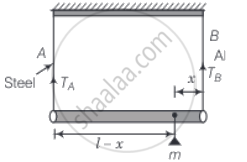
Let TA and TB be the tensions in wire A and wire B respectively.
For the rotational equilibrium of the system,
∑τ = 0 ......(Total torque = 0)
⇒ `T_Bx = T_A (l - x)` = 0
⇒ `T_B/T_A = (l - x)/x` ......(i)
Stress in wire `A = S_A = T_A/a_A`
Stress in wire `B = S_B = T_B/a_B`
Where aA and aB are cross-sectional areas of wire A and B respectively.
By question aB = 2aA
Now, for equal stress SA = SB
⇒ `T_A/a_A = T_B/a_B`
⇒ `T_B/T_A = a_B/a_A` = 2
⇒ `(l - x)/x` = 2
⇒ `l/x - 1` = 2
⇒ `x = l/3`
⇒ `l - x = l - l/3 = (2l)/3`
Hence, mass m should be placed closer to B.
For equal train, (strain)A = (strain)B
⇒ `(Y_A)/S_A = Y_B/S_B` ......(Where YA and YB are Young moduli)
⇒ `Y_(steel)/(T_A/a_A) = Y_(Al)/(T_B/a_B)`
⇒ `Y_(steel)/Y_(Al) = T_A/T_B xx a_B/a_A = (x/(l - x))((2a_A)/a_A)`
⇒ `(200 xx 10^9)/(70 xx 10^9) = (2x)/(l - x)`
⇒ `20/7 = (2x)/(l - x)`
⇒ `10/7 = x/(l - x)`
⇒ `10l - 10x = 7x`
⇒ `17x = 10l`
⇒ `x = (10l)/17`
`l - x = l - (10l)/17 = (7l)/17`
Hence, mass m should be placed closer to wire A.
APPEARS IN
RELATED QUESTIONS
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
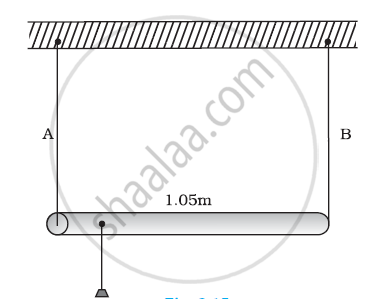
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
When the skeleton of an elephant and the skeleton of a mouse are prepared in the same size, the bones of the elephant are shown thicker than those of the mouse. Explain why the bones of an elephant are thicker than proportionate. The bones are expected to withstand the stress due to the weight of the animal.
The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two persons are pulling your legs along your own length. How much will be the increase in your length if the strain is 1% ? Do you think your yield point is 1% or much less than that?
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
Answer in one sentence.
How should be a force applied on a body to produce shearing stress?
A spiral spring is stretched by a weight. The strain will be:
A rod has a radius of 100 mm and a length of 10 cm. A 100 N force compress along its length. Calculate the longitudinal stress developed in the rod.
Modulus of rigidity of ideal liquids is ______.
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will ______.
Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1πms-2, what will be the tensile stress that would be developed in the wire?
Answer in one sentence:
What is an elastomer?
Strain is defined as the ratio of ______.
The SI unit of stress is ______.
When an elastic body is in equilibrium in its altered shape, the magnitude of the external deforming force is ______.
