Advertisements
Advertisements
Question
A load of 10 kg is suspended by a metal wire 3 m long and having a cross-sectional area 4 mm2. Find (a) the stress (b) the strain and (c) the elongation. Young modulus of the metal is 2.0 × 1011 N m−2.
Solution
Given:
Mass of the load (m) = 10 kg
Length of wire (L) = 3 m
Area of cross-section of the wire (A) = 4 mm2 = 4.0 × 10−6 m2
Young's modulus of the metal Y = 2.0 × 1011 N m−2
(a) Stress = F/A
F = mg
= \[10 \times 10\] = 100 N (g = 10 m/s2)
\[\therefore \frac{F}{A} = \frac{100}{4 \times {10}^{- 6}}\]
\[ = 2 . 5 \times {10}^7 \text{ N/ m }^2\]
(b) Strain = \[\frac{\Delta L}{L}\]
Or,
\[\text{ Strain } = \frac{\text{ Stress }}{Y}\]
\[\text{ Strain }= \frac{2 . 5 \times {10}^7}{2 \times {10}^{11}}\]
\[ = 1 . 25 \times {10}^{- 4} \text{ N/ m}^2\]
(c) Let the elongation in the wire be \[∆ L\] .
\[\text { Strain} = \frac{\Delta L}{L}\]
\[ \Rightarrow \Delta L = \left( \text{ Strain } \right) \times L\]
\[ = 1 . 25 \times {10}^{- 4} \times 3\]
\[ = 3 . 75 \times {10}^{- 4} \text{ m}\]
APPEARS IN
RELATED QUESTIONS
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
Determine the volume contraction of a solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7.0 ×106 Pa.
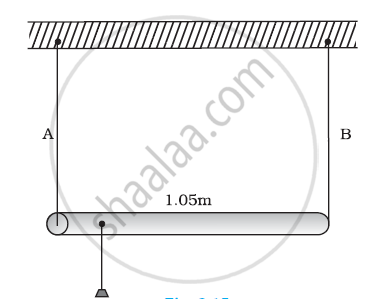
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two persons are pulling your legs along your own length. How much will be the increase in your length if the strain is 1% ? Do you think your yield point is 1% or much less than that?
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
A spiral spring is stretched by a weight. The strain will be:
A rod has a radius of 100 mm and a length of 10 cm. A 100 N force compress along its length. Calculate the longitudinal stress developed in the rod.
Modulus of rigidity of ideal liquids is ______.
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will ______.
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 × 109 Nm−2 and Ysteel = 200 × 109 Nm–2)
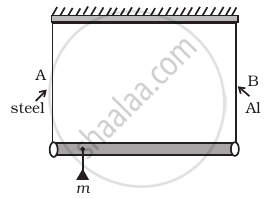
- Mass m should be suspended close to wire A to have equal stresses in both the wires.
- Mass m should be suspended close to B to have equal stresses in both the wires.
- Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
- Mass m should be suspended close to wire A to have equal strain in both wires.
Is stress a vector quantity?
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
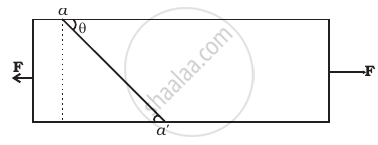
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
If 'S' is stress and 'Y' is young's modulus of the material of a wire, the energy stored in the wire per unit volume is ______.
The area of the cross-section of the rope used to lift a load by a crane is 2.5 × 10-4m2. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross-section of the rope should be ______.
(take g = 10 ms-2)
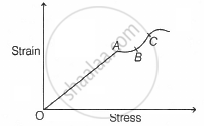
The stress-strain graph of a material is shown in the figure. The region in which the material is elastic is ______.
What is an elastomer?
