Advertisements
Advertisements
Question
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
Advertisements
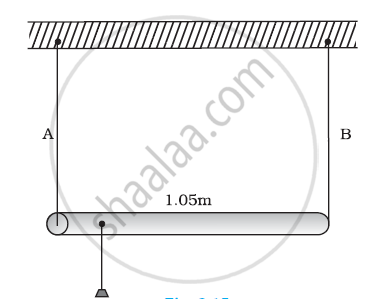
Solution 1
a) 0.7 m from the steel-wire end
Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.
Stress in wire = `"Force"/"Area"= F/a`
If the two wires have equal stresses, then:
`F_1/a_1 = F_2/a_2`
Where
F1 = Force exerted on the steel wire
F2 = Force exerted on the aluminum wire
`F_1/F_2 = a_1/a_2 = 1/2` ....(i)
The situation is shown in the following figure.
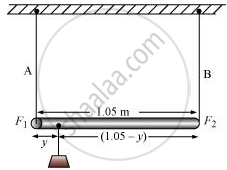
Taking torque about the point of suspension, we have:
`F_1y =F_2(1.05 - y)`
`F_1/F_2 = (1.05 - y)/y` ...(ii)
Using equations (i) and (ii), we can write:
`(1.05 -y)/y = 1/5`
2(1.05 - y) = y
2.1 - 2y = y
3y = 2.1
`:. y = 0.7 m`
In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
b) 0.432 m from the steel-wire end
Cross-sectional area of wire A, a1 = 1.0 mm2 = 1.0 × 10–6 m2
Cross-sectional area of wire B, a2 = 2.0 mm2 = 2.0 × 10–6 m2
Young’s modulus for steel, Y1 = 2 × 1011 Nm–2
Young’s modulus for aluminium, Y2 = 7.0 ×1010 Nm–2
`"Young's modulus" = "Stress"/"Strain"`
Strain = `"Stress"/"Young's modulus" = a/Y`
`(F_1/a_1)/Y_1 = (F_2/a_2)/Y_2`
`F_1/F_2 = a_1/a_2 Y_1/Y_2 = 1/2 xx (2xx10^11)/(7xx10^10) =10/7` ....(iii)
Taking torque about the point where mass m, is suspended at a distance y1 from the side where wire A attached, we get:
F1y1 = F2 (1.05 – y1)
`F_1/F_2 = (1.05 - y_1)/y_1` ...(iii)
Using equations (iii) and (iv), we get:
`((1.05 - y_1))/y_1 = 10/7`
`7(1.05 - y_1) = 10y_1`
17y_1 = 7.35
`:.y_1 = 0.432`
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached
Solution 2
For steel wire A, l1=l; Az = 1 mm2; Y1= 2 x 1011 Nm-2
For aluminium wire B, l2 = l; A2 = 2mm2; Y2 = 7 x 1010 Nm-2
a) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F1 and F2be the tensions in two wires and there is equal stress in two wires, then
`F_1/A_1 = F_2/A_2 =>F_1/F_2 =A_1/A_2 = 1/2` ... (i)
Taking moment of forces about the point of suspension of mass from the rod, we have
`F_1x = F_2(1.05 - x) or (1.05 - x)/x = F_1/F_2 = 1/2`
or 2.10 - 2x = x => x = 0.70 m = 70 cm
(b) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F1 and F2be the tension in the wires and there is equal strain in the two wires i.e.,
`F_1/(A_1Y_1) = F_2/(A_2Y_2) => F_1/F_2 = (A_1Y_1)/(A_2Y_2) = 1/2 xx (2xx10^11)/(7xx10^10) = 10/7`
As the rod is stationary, so `F_1x = F_2(1.05 - x)` or
`(1.05 - x)/x = F_1/F_2 = 10/7`
=>10x =7.35 - 7x or x= 0.4324 m = 43.2 cm
RELATED QUESTIONS
When the skeleton of an elephant and the skeleton of a mouse are prepared in the same size, the bones of the elephant are shown thicker than those of the mouse. Explain why the bones of an elephant are thicker than proportionate. The bones are expected to withstand the stress due to the weight of the animal.
The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two persons are pulling your legs along your own length. How much will be the increase in your length if the strain is 1% ? Do you think your yield point is 1% or much less than that?
When some wax is rubbed on a cloth, it becomes waterproof. Explain.
A wire can sustain the weight of 20 kg before breaking. If the wire is cut into two equal parts, each part can sustain a weight of
A heave uniform rod is hanging vertically form a fixed support. It is stretched by its won weight. The diameter of the rod is
A load of 10 kg is suspended by a metal wire 3 m long and having a cross-sectional area 4 mm2. Find (a) the stress (b) the strain and (c) the elongation. Young modulus of the metal is 2.0 × 1011 N m−2.
Answer in one sentence.
Define strain.
A charged particle is moving in a uniform magnetic field in a circular path of radius R. When the energy of the particle becomes three times the original, the new radius will be ______.
A spiral spring is stretched by a weight. The strain will be:
A rod has a radius of 100 mm and a length of 10 cm. A 100 N force compress along its length. Calculate the longitudinal stress developed in the rod.
Modulus of rigidity of ideal liquids is ______.
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (Figure). A mass m is suspended from the mid point of the wire. Strain in the wire is ______.
A wire is suspended from the ceiling and stretched under the action of a weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
- Tensile stress at any cross section A of the wire is F/A.
- Tensile stress at any cross section is zero.
- Tensile stress at any cross section A of the wire is 2F/A.
- Tension at any cross section A of the wire is F.
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 × 109 Nm−2 and Ysteel = 200 × 109 Nm–2)
- Mass m should be suspended close to wire A to have equal stresses in both the wires.
- Mass m should be suspended close to B to have equal stresses in both the wires.
- Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
- Mass m should be suspended close to wire A to have equal strain in both wires.
Is stress a vector quantity?
The value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1 and l2 respectively. The actual length of the metal wire is ______.
Strain is defined as the ratio of:
When an elastic body is in equilibrium in its altered shape, the magnitude of the external deforming force is:
