Advertisements
Advertisements
प्रश्न
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
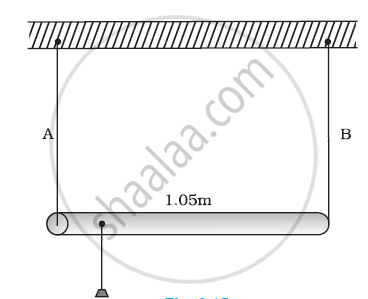
उत्तर १
a) 0.7 m from the steel-wire end
Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.
Stress in wire = `"Force"/"Area"= F/a`
If the two wires have equal stresses, then:
`F_1/a_1 = F_2/a_2`
Where
F1 = Force exerted on the steel wire
F2 = Force exerted on the aluminum wire
`F_1/F_2 = a_1/a_2 = 1/2` ....(i)
The situation is shown in the following figure.
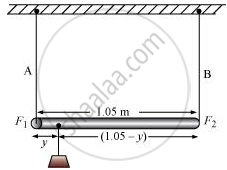
Taking torque about the point of suspension, we have:
`F_1y =F_2(1.05 - y)`
`F_1/F_2 = (1.05 - y)/y` ...(ii)
Using equations (i) and (ii), we can write:
`(1.05 -y)/y = 1/5`
2(1.05 - y) = y
2.1 - 2y = y
3y = 2.1
`:. y = 0.7 m`
In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
b) 0.432 m from the steel-wire end
Cross-sectional area of wire A, a1 = 1.0 mm2 = 1.0 × 10–6 m2
Cross-sectional area of wire B, a2 = 2.0 mm2 = 2.0 × 10–6 m2
Young’s modulus for steel, Y1 = 2 × 1011 Nm–2
Young’s modulus for aluminium, Y2 = 7.0 ×1010 Nm–2
`"Young's modulus" = "Stress"/"Strain"`
Strain = `"Stress"/"Young's modulus" = a/Y`
`(F_1/a_1)/Y_1 = (F_2/a_2)/Y_2`
`F_1/F_2 = a_1/a_2 Y_1/Y_2 = 1/2 xx (2xx10^11)/(7xx10^10) =10/7` ....(iii)
Taking torque about the point where mass m, is suspended at a distance y1 from the side where wire A attached, we get:
F1y1 = F2 (1.05 – y1)
`F_1/F_2 = (1.05 - y_1)/y_1` ...(iii)
Using equations (iii) and (iv), we get:
`((1.05 - y_1))/y_1 = 10/7`
`7(1.05 - y_1) = 10y_1`
17y_1 = 7.35
`:.y_1 = 0.432`
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached
उत्तर २
For steel wire A, l1=l; Az = 1 mm2; Y1= 2 x 1011 Nm-2
For aluminium wire B, l2 = l; A2 = 2mm2; Y2 = 7 x 1010 Nm-2
a) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F1 and F2be the tensions in two wires and there is equal stress in two wires, then
`F_1/A_1 = F_2/A_2 =>F_1/F_2 =A_1/A_2 = 1/2` ... (i)
Taking moment of forces about the point of suspension of mass from the rod, we have
`F_1x = F_2(1.05 - x) or (1.05 - x)/x = F_1/F_2 = 1/2`
or 2.10 - 2x = x => x = 0.70 m = 70 cm
(b) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F1 and F2be the tension in the wires and there is equal strain in the two wires i.e.,
`F_1/(A_1Y_1) = F_2/(A_2Y_2) => F_1/F_2 = (A_1Y_1)/(A_2Y_2) = 1/2 xx (2xx10^11)/(7xx10^10) = 10/7`
As the rod is stationary, so `F_1x = F_2(1.05 - x)` or
`(1.05 - x)/x = F_1/F_2 = 10/7`
=>10x =7.35 - 7x or x= 0.4324 m = 43.2 cm
APPEARS IN
संबंधित प्रश्न
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
The ratio stress/strain remain constant for small deformation of a metal wire. When the deformation is made larger, will this ratio increase or decrease?
A heave uniform rod is hanging vertically form a fixed support. It is stretched by its won weight. The diameter of the rod is
Modulus of rigidity of ideal liquids is ______.
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
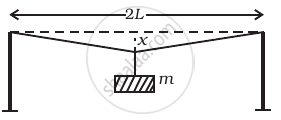
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (Figure). A mass m is suspended from the mid point of the wire. Strain in the wire is ______.
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 × 109 Nm−2 and Ysteel = 200 × 109 Nm–2)
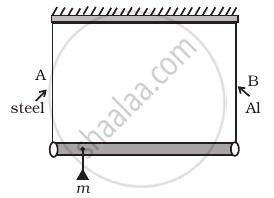
- Mass m should be suspended close to wire A to have equal stresses in both the wires.
- Mass m should be suspended close to B to have equal stresses in both the wires.
- Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
- Mass m should be suspended close to wire A to have equal strain in both wires.
The stress-strain graph of a material is shown in the figure. The region in which the material is elastic is ______.
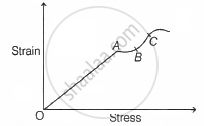
What is an elastomer?
