Question

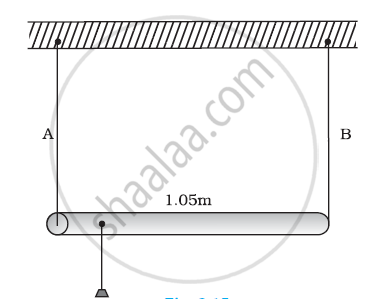
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm² and 2.0 mm², respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.

 

Answer 1

a) 0.7 m from the steel-wire end

Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.

Stress in wire = `"Force"/"Area"= F/a`

If the two wires have equal stresses, then:

`F_1/a_1 = F_2/a_2`

Where

F₁ = Force exerted on the steel wire

F₂ = Force exerted on the aluminum wire

`F_1/F_2 = a_1/a_2 = 1/2`  ....(i)

The situation is shown in the following figure.

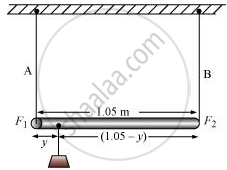
Taking torque about the point of suspension, we have:

`F_1y =F_2(1.05 - y)`

`F_1/F_2 = (1.05 - y)/y`  ...(ii)

Using equations (i) and (ii), we can write:

`(1.05 -y)/y = 1/5`

2(1.05 - y) = y

2.1 - 2y = y

3y = 2.1

`:. y = 0.7 m`

In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.

b) 0.432 m from the steel-wire end

Cross-sectional area of wire A, a₁ = 1.0 mm² = 1.0 × 10^–6 m²

Cross-sectional area of wire B, a₂ = 2.0 mm² = 2.0 × 10^–6 m²

Young’s modulus for steel, Y₁ = 2 × 10¹¹ Nm^–2

Young’s modulus for aluminium, Y₂ = 7.0 ×10¹⁰ Nm^–2

`"Young's modulus" = "Stress"/"Strain"`

Strain = `"Stress"/"Young's modulus" = a/Y`

`(F_1/a_1)/Y_1 = (F_2/a_2)/Y_2`

`F_1/F_2 = a_1/a_2 Y_1/Y_2 = 1/2 xx (2xx10^11)/(7xx10^10) =10/7`   ....(iii)

Taking torque about the point where mass m, is suspended at a distance y₁ from the side where wire A attached, we get:

F₁y₁ = F₂ (1.05 – y₁)

`F_1/F_2 = (1.05 - y_1)/y_1`  ...(iii)

Using equations (iii) and (iv), we get:

`((1.05 - y_1))/y_1 = 10/7`

`7(1.05 - y_1) = 10y_1`

17y_1 = 7.35

`:.y_1 = 0.432`

In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached

Answer 2

For steel wire A, l₁=l; A_z = 1 mm²; Y₁= 2 x 1011 Nm^-2

For aluminium wire B, l₂ = l; A₂ = 2mm²; Y₂ = 7 x 1010 Nm^-2

a) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F₁ and F₂be the tensions in two wires and there is equal stress in two wires, then

`F_1/A_1 = F_2/A_2 =>F_1/F_2 =A_1/A_2 = 1/2`  ... (i)

Taking moment of forces about the point of suspension of mass from the rod, we have

`F_1x = F_2(1.05 - x) or (1.05 - x)/x = F_1/F_2 = 1/2`

or 2.10 - 2x = x => x = 0.70 m = 70 cm

(b) Let mass m be suspended from the rod at distance x from the end where wire A is connected. Let F₁ and F₂be the tension in the wires and there is equal strain in the two wires i.e.,

`F_1/(A_1Y_1) = F_2/(A_2Y_2) => F_1/F_2 = (A_1Y_1)/(A_2Y_2) = 1/2 xx (2xx10^11)/(7xx10^10) = 10/7`

As the rod is stationary, so `F_1x = F_2(1.05 - x)` or

`(1.05 - x)/x = F_1/F_2 = 10/7`

=>10x =7.35 - 7x or x= 0.4324 m = 43.2 cm