Advertisements
Advertisements
प्रश्न
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
उत्तर १
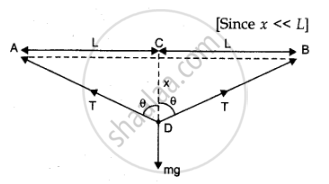
Let AB be a mild steel wire of length 2L = lm and its cross-section area A = 0.50 x 10-2 cm2. A mass m = 100 g = 0.1 kg is suspended at mid-point C of wire as shown in figure. Let x be the depression at mid-point i.e., CD = x
`:. AD = DB = sqrt((AC^2 + CD^2)) = sqrt(L^2+x^2)`
:. Increase in length `triangleL = (AD+DB) - AB = 2sqrt(L^2+x^2) - 2L`
`= 2L[(1+x^2/L^2)^(1/2) - 1] = 2L.x^2/(2L^2) = x^2/L`
:. Longitudinal strain = `(triangleL)/(2L) = x^2/(2L^2)`
If T be the tension in the wire as shown figure then in equilibrium `2T cos theta = mg`
or `T = "mg"/(2costheta)`
`= "mg"/(2 x/(sqrt(x^2+L^2))) = (mgsqrt(x^2+L^2))/(2x) = "mgL"/(2x)`
:. Stress = `T/A = "mgL"/(2 x A)`
As Young's modulus Y = `"stress"/"strain"`
`=((mgL)/(2 x A))/((x^2)/(2L^2)) = (mgL)/(2 x A) xx (2L^2)/x^2 = (mgL^3)/(Ax^3)`
`=> x = [(mgL^3)/(YA)]^(1/3) = L[(mg)/(YA)]^(1/3)`
`= 1/2[(0.1xx9.8)/(2xx10^11xx0.50xx10^(-2)xx10^(-4))]^(1/3) = 1.074 xx 10^(-2) m`
= 1.074 cm ≈ 1.07 cm or 0.01 m
उत्तर २

Length of the steel wire = 1.0 m
Area of cross-section, A = 0.50 × 10–2 cm2 = 0.50 × 10–6 m2
A mass 100 g is suspended from its midpoint.
m = 100 g = 0.1 kg
Hence, the wire dips, as shown in the given figure.
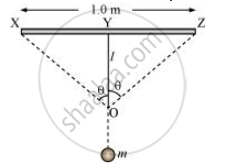
Original length = XZ
Depression = l
The length after mass m is attached to the wire = XO + OZ
Increase in the length of the wire:
Δl = (XO + OZ) – XZ
Where,
XO = OZ = `[(0.5)^2 + l^2]^(1/2)`
`:.triangle l = 2[(0.5)^2 + (l)^2]^(1/2) - 1.0`
`= 2 xx 0.5 [1+(l/0.5)^2]^(1/2) - 1.0`
Expanding and neglecting higher terms, we get
`triangle l = l^2/0.5`
`"Strain" = "Increase in length"/"Original length"`
Let T be the tension in the wire.
∴mg = 2T cosθ
Using the figure, it can be written as:
`cos theta = l/((0.5)^2 + l^2)^(1/2)`
`= l/ ((0.5)(1+(l/0.5)^2)^(1/2))`
Expanding the expression and eliminating the higher terms:
`cos theta = l/((0.5)(1+l^2/(2(0.5)^2)))`
`(1+l^2/(0.5))=~1` for small l
`:. cos theta = l/(0.5)`
`:. T = (mg)/(2(l/(0.5))) = (mgxx 0.5)/(2l) = (mg)/(4l)`
`"Stress" = "Tension"/"Area" = (mg)/(4lxxA)`
`Y = (mg xx 0.5)/(4lxxAxxl^2)`
`l = sqrt((mgxx0.5)/(4YA)) `
Young’s modulus of steel, Y = 2 x 1011 Pa
`:.l = sqrt((0.1xx9.8xx0.5)/(4xx2xx10^11xx0.50xx10^(-6)))`
= 0.0106 m
Hence, the depression at the midpoint is 0.0106 m.
APPEARS IN
संबंधित प्रश्न
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107 Pa? Assume that each rivet is to carry one-quarter of the load.
The ratio stress/strain remain constant for small deformation of a metal wire. When the deformation is made larger, will this ratio increase or decrease?
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
A wire can sustain the weight of 20 kg before breaking. If the wire is cut into two equal parts, each part can sustain a weight of
A heave uniform rod is hanging vertically form a fixed support. It is stretched by its won weight. The diameter of the rod is
A load of 10 kg is suspended by a metal wire 3 m long and having a cross-sectional area 4 mm2. Find (a) the stress (b) the strain and (c) the elongation. Young modulus of the metal is 2.0 × 1011 N m−2.
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) | 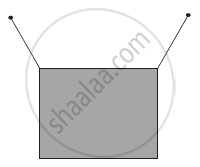 |
| (b) |  |
| (c) | 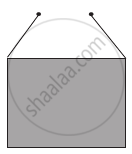 |
The tension in the strings will be ______.
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1πms-2, what will be the tensile stress that would be developed in the wire?
A body of mass m = 10 kg is attached to one end of a wire of length 0.3 m. The maximum angular speed (in rad s-1) with which it can be rotated about its other end in the space station is (Breaking stress of wire = 4.8 × 107 Nm-2 and the area of cross-section of the wire = 10-2 cm2) is ______.
Answer in one sentence:
What is an elastomer?
