Advertisements
Advertisements
Question
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
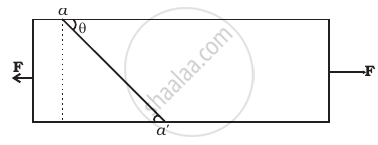
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
Solution
Consider the adjacent diagram,
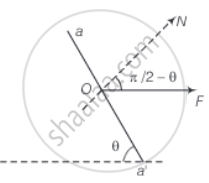
Let the cross-sectional area of the bar be A. COnsider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle `pi/2 - theta` with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
`F_p = F cos θ`
`F_N = F sin θ`
Let the area of the face aa' be A, then
`A/A^' = sin θ`
∴ `A^' = A/sin θ`
The tensile stress = `"Normal force"/"Area" = (F sin θ)/A^'`
= `(F sin θ)/(A/sin θ)`
= `F/A sin^2 θ`
Shearing stress = `"Parallel force"/"Area"`
= `(F sin θ)/(A/sin θ)`
= `F/A sin θ. cos θ`
= `F/(2A) (2 sin θ. cos θ)`
= `F/(2A) sin 2θ`
a. For tensile stress to be maximum, `sin^2theta` = 1
⇒ `sin θ` = 1
⇒ θ = `pi/2`
b. For shearing stress to be maximum,
sin 2θ = 1
⇒ 2θ = `pi/2`
⇒ θ = `pi/4`
APPEARS IN
RELATED QUESTIONS
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
A load of 10 kg is suspended by a metal wire 3 m long and having a cross-sectional area 4 mm2. Find (a) the stress (b) the strain and (c) the elongation. Young modulus of the metal is 2.0 × 1011 N m−2.
Answer in one sentence.
Define strain.
A charged particle is moving in a uniform magnetic field in a circular path of radius R. When the energy of the particle becomes three times the original, the new radius will be ______.
Modulus of rigidity of ideal liquids is ______.
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will ______.
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) | 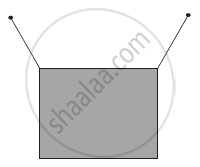 |
| (b) |  |
| (c) | 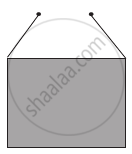 |
The tension in the strings will be ______.
Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
The area of the cross-section of the rope used to lift a load by a crane is 2.5 × 10-4m2. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross-section of the rope should be ______.
(take g = 10 ms-2)
