Advertisements
Advertisements
प्रश्न
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
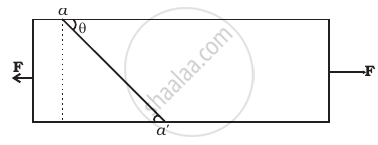
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
उत्तर
Consider the adjacent diagram,
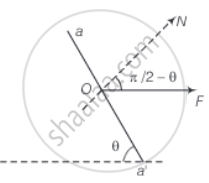
Let the cross-sectional area of the bar be A. COnsider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle `pi/2 - theta` with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
`F_p = F cos θ`
`F_N = F sin θ`
Let the area of the face aa' be A, then
`A/A^' = sin θ`
∴ `A^' = A/sin θ`
The tensile stress = `"Normal force"/"Area" = (F sin θ)/A^'`
= `(F sin θ)/(A/sin θ)`
= `F/A sin^2 θ`
Shearing stress = `"Parallel force"/"Area"`
= `(F sin θ)/(A/sin θ)`
= `F/A sin θ. cos θ`
= `F/(2A) (2 sin θ. cos θ)`
= `F/(2A) sin 2θ`
a. For tensile stress to be maximum, `sin^2theta` = 1
⇒ `sin θ` = 1
⇒ θ = `pi/2`
b. For shearing stress to be maximum,
sin 2θ = 1
⇒ 2θ = `pi/2`
⇒ θ = `pi/4`
APPEARS IN
संबंधित प्रश्न
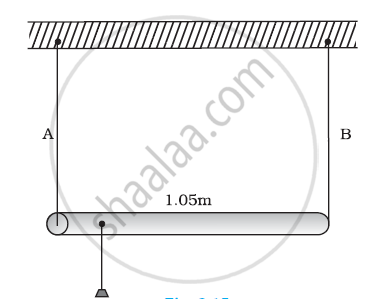
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
When a metal wire is stretched by a load, the fractional change in its volume ∆V/V is proportional to
Answer in one sentence.
Define strain.
A wire is suspended from the ceiling and stretched under the action of a weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
- Tensile stress at any cross section A of the wire is F/A.
- Tensile stress at any cross section is zero.
- Tensile stress at any cross section A of the wire is 2F/A.
- Tension at any cross section A of the wire is F.
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1πms-2, what will be the tensile stress that would be developed in the wire?
The area of the cross-section of the rope used to lift a load by a crane is 2.5 × 10-4m2. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross-section of the rope should be ______.
(take g = 10 ms-2)
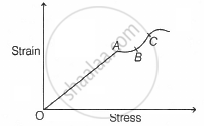
The stress-strain graph of a material is shown in the figure. The region in which the material is elastic is ______.
What is an elastomer?
