Advertisements
Advertisements
प्रश्न
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
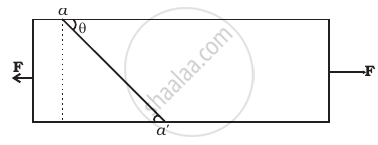
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
उत्तर
Consider the adjacent diagram,
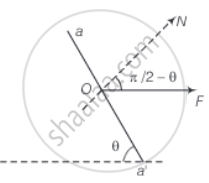
Let the cross-sectional area of the bar be A. COnsider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle `pi/2 - theta` with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
`F_p = F cos θ`
`F_N = F sin θ`
Let the area of the face aa' be A, then
`A/A^' = sin θ`
∴ `A^' = A/sin θ`
The tensile stress = `"Normal force"/"Area" = (F sin θ)/A^'`
= `(F sin θ)/(A/sin θ)`
= `F/A sin^2 θ`
Shearing stress = `"Parallel force"/"Area"`
= `(F sin θ)/(A/sin θ)`
= `F/A sin θ. cos θ`
= `F/(2A) (2 sin θ. cos θ)`
= `F/(2A) sin 2θ`
a. For tensile stress to be maximum, `sin^2theta` = 1
⇒ `sin θ` = 1
⇒ θ = `pi/2`
b. For shearing stress to be maximum,
sin 2θ = 1
⇒ 2θ = `pi/2`
⇒ θ = `pi/4`
APPEARS IN
संबंधित प्रश्न
The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two persons are pulling your legs along your own length. How much will be the increase in your length if the strain is 1% ? Do you think your yield point is 1% or much less than that?
When a metal wire is stretched by a load, the fractional change in its volume ∆V/V is proportional to
Answer in one sentence.
How should be a force applied on a body to produce shearing stress?
A spiral spring is stretched by a weight. The strain will be:
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) | 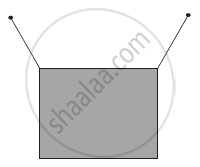 |
| (b) |  |
| (c) | 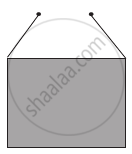 |
The tension in the strings will be ______.
Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1πms-2, what will be the tensile stress that would be developed in the wire?
The stress-strain graph of a material is shown in the figure. The region in which the material is elastic is ______.
Answer in one sentence:
What is an elastomer?
