Advertisements
Advertisements
Question
A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2 R where R= 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R ?
[G = 6.67 × 10–11 SI units and M = 6 × 1024 kg]
Advertisements
Solution
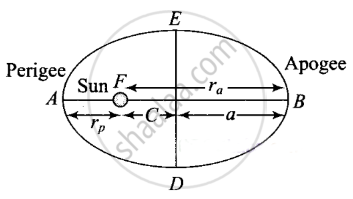
According to the diagram,
rp = radius of perigee = 2R
ra = radius of perigee = 6R
a = semi-major axis of the ellipse
Hence, we can write
`r_a = a(1 + e) = 6R`
`r_p = a(1 - e) = 2R`
`(a(1 + e))/(a(1 - e)) = (6R)/(2R)` = 3
By solving, we get eccentricity `e = 1/2`
If va and vp are the velocities of the satellite (of mass m) at aphelion and perihelion respectively, then by conservation of angular momentum
`L_("at perigee") = L_("at apogee")`
∴ `mv_pr_p = mv_ar_a`
∴ `v_a/v_p = r_p/r_a = 1/3`
Applying conservation of energy,
The energy at perigee = Energy at apogee
`1/2 mv_p^2 - (GMm)/r_p = 1/2 mv_a^2 - (GMm)/r_a`
Where M is the mass of the earth
∴ `v_p^2 (1 - 1/9) = - 2GM (1/r_a - 1/r_p)`
= `2GM(1/r_p - 1/r_a)` .....(By putting `v_a = v_p/3`)
`v_p = [2GM(1/r_p - 1/r_a)]^(1/2)/([1 - (v_a/v_p)^2]^(1/2)`
= `[((2GM)/R (1/2 - 1/6))/((1 - 1/9))]^(1/2)`
= `((2/3)/(8/9) (GM)/R)^(1/2)`
= `sqrt(3/4 (GM)/R)`
= 6.85 km/s
vp = 6.885 km/s, va = 2.28 km/s
For circular orbit of radius r,
vc = orbital velocity = `sqrt((GM)/r)`
For r = 6R, vc = `sqrt((GM)/(6R)` = 3.23 km/s.
APPEARS IN
RELATED QUESTIONS
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be \[\sqrt{8}\] T.
Answer the following question.
State Kepler’s law of the period.
Observe the given figure showing the orbit of a planet moving around the Sun and write the three laws related to it:
The orbit of a planet moving around the Sun
Observe the given figure and answer these following questions.
The orbit of a planet moving around the Sun
- What is the conclusion about the orbit of a planet?
- What is the relation between velocity of planet and distance from sun?
- Explain the relation between areas ASB, CSD and ESF.
The mass and radius of earth is 'Me' and 'Re' respectively and that of moon is 'Mm' and 'Rm' respectively. The distance between the centre of the earth and that of moon is 'D'. The minimum speed required for a body (mass 'm') to project from a point midway between their centres to escape to infinity is ______.
The earth moves around the sun in an elliptical orbit as shown in the figure. The ratio, `"OA"/"OB"` = x. The ratio of the speed of the earth at Band at A is ______.
A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b, then the time period is given by:
If the sun and the planets carried huge amounts of opposite charges ______.
- all three of Kepler’s laws would still be valid.
- only the third law will be valid.
- the second law will not change.
- the first law will still be valid.
The centre of mass of an extended body on the surface of the earth and its centre of gravity ______.
- are always at the same point for any size of the body.
- are always at the same point only for spherical bodies.
- can never be at the same point.
- is close to each other for objects, say of sizes less than 100 m.
- both can change if the object is taken deep inside the earth.
Give one example each of central force and non-central force.
Draw areal velocity versus time graph for mars.
A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
A planet revolving in an elliptical orbit has:
- a constant velocity of revolution.
- has the least velocity when it is nearest to the sun.
- its areal velocity is directly proportional to its velocity.
- areal velocity is inversely proportional to its velocity.
- to follow a trajectory such that the areal velocity is constant.
Choose the correct answer from the options given below:
Two planets A and B of equal mass are having their period of revolutions TA and TB such that TA = 2TB. These planets are revolving in the circular orbits of radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits?
How can an ellipse be drawn using pins and thread?
What is at one focus of the elliptical orbit of a planet?
When is a planet moving fastest in its orbit?
