Advertisements
Advertisements
Question
A series CR circuit with R = 200 Ω and C = (50/π) µF is connected across an ac source of peak voltage ε0 = 100 V and frequency v = 50 Hz. Calculate (a) impedance of the circuit (Z), (b) phase angle (Φ), and (c) voltage across the resistor.
Solution
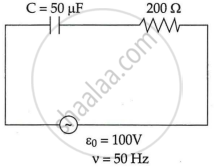
(a) Given: R = 200Ω, C = `50/pi` μF, ε0 = 100V, Frequency(ν) = 50Hz
We know that the reactance of a capacitor (XC) is given by the formula.
XC = `1/((omegaC))`
where C is the capacitance and ω = 2πν.
∴ XC = `1/(omegaC) = 1/(2piνC)`
XC = `1/((2pi xx 50 xx 50"/"pi xx 10^-6))`
XC = `10^6/((2 xx 50 xx 50))`
XC = 200 Ω
R = 200 Ω
The impedance of the circuit can be calculated by the given formula,
`Z^2 = R^2 + X_{C^2}`
`Z^2 = (200)^2 + (200)^2`
Z = `200sqrt2Omega`
(b) The phase angle can be calculated as
`tanphi = X_C/R`
`tanphi = 200/200`
`tanphi` = 1
Φ = 45°
(c) Voltage across the resistor can be calculated as,
ε0 = 100 V
`I_("r.m.s.") = E_("r.m.s.")/Z = 100/(200sqrt2)`
`(V_"r.m.s.")_R = I_("r.m.s.") xx R`
`(V_"r.m.s.")_R = (E_"r.m.s." xx R)/Z`
`(V_"r.m.s.")_R = 100/((sqrt2 xx 200sqrt2)) xx 200`
`(V_"r.m.s.")_R = 100/2`
`(V_"r.m.s.")_R = 50` V
APPEARS IN
RELATED QUESTIONS
In a series RL circuit, the resistance and inductive reactance are the same. Then the phase difference between the voltage and current in the circuit is
How will you define RMS value of an alternating current?
Define capacitive reactance. Give its units.
Calculate the instantaneous value at 60°, average value and RMS value of an alternating current whose peak value is 20 A.
Which of the following is independent of the frequency of a.c?
For a series LCR circuit, I vs ω curve is shown:
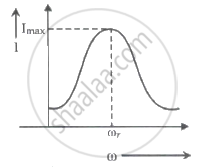
- To the left of ωr, the circuit is mainly capacitive.
- To the left of ωr, the circuit is mainly inductive.
- At ωr, impedance of the circuit is equal to the resistance of the circuit.
- At ωr, impedance of the circuit is 0.
An inductor coil stores 64 J of magnetic field energy and dissipates energy at the rate of 640 W when a current of 8 A is passed through it. If this coil is joined across an ideal battery, find the time constant of the circuit in seconds ______.
The r.m.s. value of alternating current is 10 A, having frequency of 50 Hz. The time taken by the current to increase from zero to maximum and the maximum value of current will be ______.
