Advertisements
Advertisements
Question
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
Solution
Let the cost price of the saree and the list price of the sweater be ₹ x and ₹ y, respectively.
Case I: Sells a saree at 8% profit + Sells a sweater at 10% discount = ₹ 1008
⇒ (100 + 8)% of x + (100 – 10)% of y = 1008
⇒ 108% of x + 90% of y = 1008
⇒ 1.08x + 0.9y = 1008 ......(i)
Case II: Sold the saree at 10% profit + Sold the sweater at 8% discount = ₹ 1028
⇒ (100 + 10)% of x + (100 – 8)% of y = 1028
⇒ 110% of x + 92% of y = 1028
⇒ 1.1x + 0.92y = 1028 .....(ii)
On putting the value of y from equation (i) into equation (ii), we get
`1.1 xx 0.92((1008 - 1.08x)/0.9)`
⇒ 1.1 × 0.9x + 927.36 – 0.9936x = 1028 × 0.9
⇒ 0.99x – 0.9936x = 925.2 – 927.36
⇒ –0.0036x = –2.16
∴ x = `2.16/0.0036` = 600
On putting the value of x in equation (i), we get
1.08 × 600 + 0.9y = 1008
⇒ 648 + 0.9y = 1008
⇒ 0.9y = 1008 – 648
⇒ 0.9y = 360
⇒ y = `360/0.9` = 400
Hence, the cost price of the saree and the list price (price before discount) of the sweater are ₹ 600 and ₹ 400, respectively.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by cross-multiplication method.
2x + 3y + 8 = 0
4x + 5y + 14 = 0
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
x – 3y – 7 = 0
3x – 3y – 15 = 0
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solve the following systems of equations:
`x + 2y = 3/2`
`2x + y = 3/2`
Solve the following systems of equations:
`2x - 3/y = 9`
`3x + 7/y = 2, y != 0`
Solve the following systems of equations:
`(7x - 2y)/"xy" = 5`
`(8x + 7y)/"xy" = 15`
Solve each of the following systems of equations by the method of cross-multiplication :
`57/(x + y) + 6/(x - y) = 5`
`38/(x + y) + 21/(x - y) = 9`
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
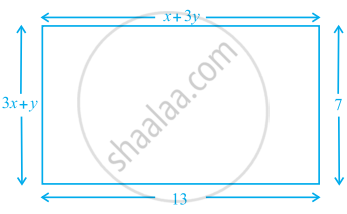
Find the values of x and y in the following rectangle [see figure].