Advertisements
Advertisements
Question
A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
Solution
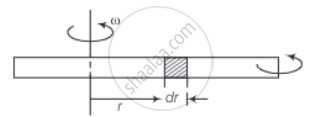
Consider an element of width dr at t as shown in the diagram.
Let T(r) and T(r + dr) be the tensions at r and r + dr respectively.
Net centrifugal force on the element = ω2rdm ....(Where ω is the angular velocity of the rod)
= ω2rμdr .....(∵ μ = mass/length)
⇒ T(r) – T(r + dr) = μω2rdr
⇒ – dT = μω2rdr ......[∵ Tension and centrifugal forces are opposite]
∴ `- int_(T = 0)^T dT = int_(r = l)^(r= r) μω^2rdr` ......[∵ T = 0 at r = l]
⇒ `T(r) = (μω^2)/2 (l^2 - r^2)`
Let the increase in length of the element dr be Δr
So, Young's modulus Y = `"Stress"/"Strain" = ((T(r))/A)/((Δr)/(dr))`
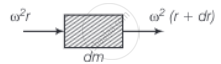
∴ `(Δr)/(dr) = (T(r))/A = (μω^2)/(2YA) (l^2 - r^2)`
∴ `Δr = 1/(YA) (μω^2)/2 (l^2 - r^2)dr`
∴ Δ = Change in length in right part = `1/(YA) (μω^2)/2 int_0^l (l^2 - r^2) dr`
= `(1/(YA)) (μω^2)/2 [t^3 - l^3/3]`
= `1/(3YA) μω^2l^2`
∴ Total change in length = 2Δ = `2/(3YA) μω^2l^2`
APPEARS IN
RELATED QUESTIONS
The stress-strain graphs for materials A and B are shown in Figure
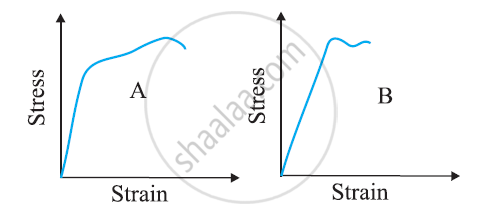
The graphs are drawn to the same scale.
(a) Which of the materials has the greater Young’s modulus?
(b) Which of the two is the stronger material?
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.

Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
A wire elongates by 1.0 mm when a load W is hung from it. If this wire goes over a a pulley and two weights W each are hung at the two ends, he elongation of he wire will be
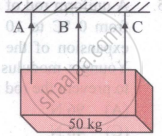
A uniform rectangular block of mass of 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2m and 10mm2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of material of Young's modulus 7.5 x 1010 Nm−2 and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 1011 Nm−2 The tension in the wires A and B will be in the ratio of:
Young's modulus of a perfectly rigid body is ______.
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
What is the Young’s modulus for a perfect rigid body ?
A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y = 2 × 1011 Nm–2).
A uniform metal rod of 2 mm2 cross section is heated from 0°C to 20°C. The coefficient of linear expansion of the rod is 12 × 10-6/°C, it's Young's modulus is 1011 N/m2. The energy stored per unit volume of the rod is ______.
