Advertisements
Advertisements
Question
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
Solution

Radius of the cylindrical tent (r) = 14 m
Total height of the tent = 13.5 m
Height of the cylinder = 3 m
Height of the conical part = 10.5 m
Slant height of the cone (l) = `sqrt(h^2 + r^2)`
= `sqrt((10.5)^2 + (14)^2`
= `sqrt(110.25 + 196)`
= `sqrt(306.25)`
= 17.5 m
Curved surface area of cylindrical portion
= 2πrh
= `2 xx 22/7 xx 14 xx 3`
= 264 m2
Curved surface area of conical portion
= πrl
= `22/7 xx 14 xx 17.5`
= 770 m2
Total curved surface area = 264 m2 + 770 m2 = 1034 m2
Provision for stitching and wastage = 26 m2
Area of canvas to be purchased = 1060 m2
Cost of canvas = Rate × Surface area
= 500 × 1060
= ₹ 5,30,000/-
APPEARS IN
RELATED QUESTIONS
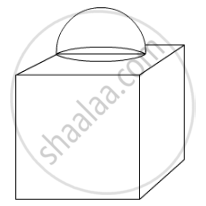
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is ______.
