Advertisements
Advertisements
Question
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
Solution
Given:
Frequency of whistle \[f_0\]= 16 × 103 Hz
Apparent frequency \[f\]= 20 × 103 Hz
(f is greater than that value)
Velocity of source \[v_s\]= 0
Let
\[v_0\]be the velocity of the observer.
Apparent frequency \[\left( f \right)\] is givne by :
\[f = \left( \frac{v + v_0}{v - v_s} \right) f_0\]
On substituting the values in the above equation, we get:
\[20 \times {10}^3 = \left( \frac{330 + v_0}{330 - 0} \right) \times 16 \times {10}^3 \]
\[ \Rightarrow \left( 330 + v_0 \right) = \frac{20 \times 330}{16}\]
\[ \Rightarrow v_0 = \frac{20 \times 330 - 16 \times 330}{4}\]
\[ = \frac{330}{4}\text { m/s } = 297 \text { km/h }\]
(b) This speed is not practically attainable for ordinary cars.
APPEARS IN
RELATED QUESTIONS
In a stationary wave,
(a) all the particles of the medium vibrate in phase
(b) all the antinodes vibrates in phase
(c) the alternate antinodes vibrate in phase
(d) all the particles between consecutive nodes vibrate in phase.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
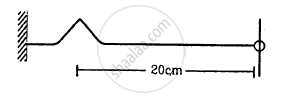
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
Change in temperature of the medium changes ______.
