Advertisements
Advertisements
Question
A train starts from rest and accelerates uniformly at a rate of 2 m s-2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and comes to rest in 50 s. Find
(i) The maximum velocity reached,
(ii) The retardation in the last 50 s,
(iii) The total distance travelled,
(iv) The average velocity of the train.
Solution
(i) For the first 10 s, initial velocity u = 0
Acceleration a = 2 m/s2
Time taken t = 10 s
Let 'v' be the maximum velocity reached.
Using the first equation of motion
v = u + at
We get
V = (0) + (2) (10) = 20 m/s-1
(ii) For the last 50 s: Final velocity = 0 m/s, initial velocity = 20 m/s.
Acceleration = (Final velocity - Initial velocity)/time
= (0 - 20)/50 = -0.4 m/s2
Retardation = 0.4 m/s-2
(iii) Total distance travelled = Distance travelled in the first 10 s + Distance travelled in 200 s + Distance travelled in last 50 s
Distance travelled in first 10s (s1) = ut + (1/2) at2
S1= (0) + (1/2) (2) (10)2
S1= 100 m
Distance travelled in 200s (s2) = speed × time
S2 = (20) (200) = 4000 m
Distance travelled in last 50s (s3) = ut + (1/2) at2
Here, u = 20 m/s, t = 50 s and a = -0.4 m/s2
S3= (20)(50) + (1/2) (-0.4) (50)2
S3= 1000 - 500
S3= 500 m
Therefore, total distance travelled = S1 + S2 + S3 = 100 + 4000 + 500 = 4600 m
(iv) Average velocity = Total distance travelled/total time taken
= (4600/260) m/s
= 17.69 m/s-1
APPEARS IN
RELATED QUESTIONS
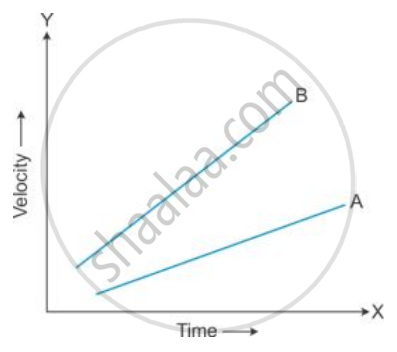
Figure shows the velocity-time graphs for two cars A and B moving in the same direction. Which car has greater acceleration? Give reasons to your answer.
A space craft flying in a straight course with velocity of 75 km s-1 fires its rocket motors for 6.0 s. At the end of this time its speed is 120 km s-1 in the same direction.
Find
(i) The space craft's average acceleration while the motors were firing
(ii) The distance travelled by the space craft in the first 10 s after the rocket motors were started, the motors being in action for only 6 s.
A car travels with uniform velocity of 25 m s-1 for 5 s. The brakes are then applied and the car is uniformly retarded and comes to rest in further 10 s. Find:
- The distance which the car travels before the brakes are applied,
- Retardation and
- The distance travelled by car after applying the brakes.
Give an example of an accelerated body, moving with a uniform speed.
A cyclist driving at 5 ms−1, picks a velocity of 10 ms−1, over a distance of 50 m. Calculate
- acceleration
- time in which the cyclist picks up above velocity.
A cyclist driving at 36 kmh−1 stops his motion in 2 s, by the application of brakes. Calculate
- retardation
- distance covered during the application of brakes.
The acceleration of a body is 8.5 ms-2. What does this statement mean?
Negative acceleration is called ______.
If the velocity of a body does not change, then its acceleration is ______.
Assertion: Position-time graph of a stationary object is a straight line parallel to the time axis.
Reason: For a stationary object, the position does not change with time.
