Advertisements
Advertisements
Question
A cyclist driving at 5 ms−1, picks a velocity of 10 ms−1, over a distance of 50 m. Calculate
- acceleration
- time in which the cyclist picks up above velocity.
Solution
Initial velocity = u = 5 ms−1
Final velocity = v = 10 ms−1
Distance = S =50 m
(i) v2 – u2 = 2aS
(10)2 – (5)2 = 2a (50)
100 − 25 = 100a
100a = 75
a = `75/100` = 0.75 ms−2
∴ Acceleration = a = 0.75 ms−2
(ii) v = u + at
10 = 5 + 0.75t
0.75t = 10 − 5 = 5
(Time) t = `5/0.75` = 6.67 S
APPEARS IN
RELATED QUESTIONS
The velocity-time graph for a uniformly retarded body is a straight line inclined to the time axis with an obtuse angle. How is retardation calculated from the velocity-time graph?
A train starts from rest and accelerates uniformly at a rate of 2 m s-2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and comes to rest in 50 s. Find
(i) The maximum velocity reached,
(ii) The retardation in the last 50 s,
(iii) The total distance travelled,
(iv) The average velocity of the train.
A ball is rolling from A to D on a flat and smooth surface. Its speed is 2 cm/s. On reaching B, it was pushed continuously up to C. On reaching D from C, its speed had become 4 cm/s. It took 2 seconds for it to go from B to C. What is the acceleration of the ball as it goes from B to C?
A motor bike running at 90 kmh−1 is slowed down to 18 kmh−1 in 2.5 s. Calculate
- acceleration
- distance covered during slow down.
A cyclist driving at 36 kmh−1 stops his motion in 2 s, by the application of brakes. Calculate
- retardation
- distance covered during the application of brakes.
A car traveling at 60 km/h, stops on applying brakes in 10 seconds. What is its acceleration?
State if the following situation is possible:
A body moving with constant acceleration but with Zero velocity.
A car accelerates to a velocity of 30 m/s in 10 s and then decelerates for 20 s so that it stops. Draw a velocity-time graph to represent the motion and find:
The acceleration.
Figure represents graphically the velocity of a car moving along a straight road over a period of 100 hours.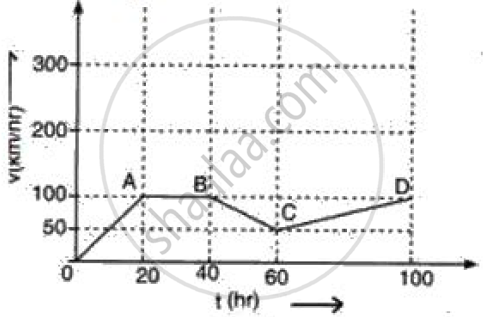
Calculate the acceleration along AB and the retardation along BC.
Acceleration is a scalar.
