Advertisements
Advertisements
Question
एका समभुज त्रिकोणाची उंची `sqrt(3)` सेमी आहे, तर त्या त्रिकोणाच्या बाजूची लांबी व परिमिती काढा.
Solution
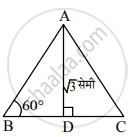
समजा, ΔABC हा समभुज त्रिकोण आहे.
∴ ∠B = 60° ....[समभुज त्रिकोणाचा कोन]
AD ⊥ BC, B-D-C
ΔABD मध्ये, ∠B = 60°, ∠ADB = 90°
∴ ∠BAD = 30° ...[त्रिकोणाचा उर्वरित कोन]
∴ ΔABD हा 30° - 60° - 90° त्रिकोण आहे.
∴ AD = `sqrt(3)/2`AB .....[60° कोनासमोरील बाजू]
∴ `sqrt(3) = sqrt(3)/2`AB
∴ AB = `(2sqrt(3))/sqrt(3)`
∴ AB = 2 सेमी
∴ समभुज त्रिकोणाची बाजू = 2 सेमी
ΔABC ची परिमिती = 3 × बाजू
= 3 × AB
= 3 × 2
= 6 सेमी
∴ दिलेल्या समभुज त्रिकोणाच्या बाजूंची लांबी व परिमिती अनुक्रमे 2 सेमी व 6 सेमी आहेत.
APPEARS IN
RELATED QUESTIONS
आकृती मधील ΔPSR मध्ये दिलेल्या माहितीवरून RP आणि PS काढा.
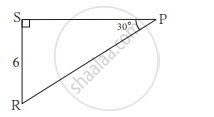
ΔRST मध्ये, ∠S = 90°, ∠T = 30°, RT = 12 सेमी तर RS व ST काढा.
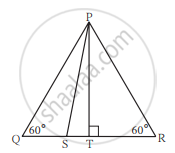
आकृती मध्ये ΔPQR हा समभुज त्रिकोण असून बिंदू S हा रेख QR वर अशा प्रकारे आहे की, QS = `1/3` QR तर सिद्ध करा; 9PS2 = 7PQ2
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
∆ABC मध्ये, AB = `6sqrt3` सेमी, AC = 12 सेमी आणि BC = 6 सेमी, तर ∠A चे माप किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AB ⊥ BC, AB = BC, तर ∠A चे माप किती?
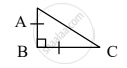
सोबतच्या आकृतीत, ∆ABC मध्ये, AB = BC, AC = `2sqrt2`, ∠ABC = 90°. तर AB ची लांबी किती?

बाजूच्या आकृतीवरून जर AQ = 8 सेमी, तर AB ची लांबी काढा.
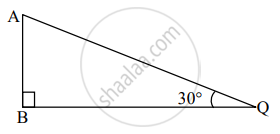
सोबतच्या आकृतीवरून, जर AC = 12 सेमी, तर AB ची लांबी काढण्यासाठी खालील कृती पूर्ण करा.
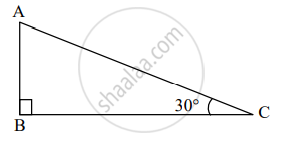
कृती: सोबतच्या आकृतीत, ∆ABC मध्ये, ∠ABC = 90°, ∠ACB = 30° यावरून,
∠BAC = `square`
म्हणजेच, ∆ABC हा 30° – 60° – 90° त्रिकोण आहे.
∆ABC मध्ये 30° – 60° – 90° त्रिकोणाच्या प्रमेयानुसार,
AB = `1/2"AC"` व `square` = `sqrt3/2"AC"`.
∴ `square` = `1/2 xx 12` व BC = `sqrt3/2 xx 12`
∴ `square` = 6 व BC = `6sqrt3.`
सोबतच्या आकृतीत, ∆ABC मध्ये, ∠ABC = 90°, ∠CAB = 30° AC = 14, तर AB व BC काढण्यासाठी खालील कृती पूर्ण करा.
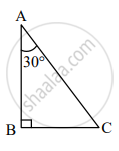
कृती: ∆ABC मध्ये, ∠ABC = 90°, ∠CAB = 30° यावरून, ∠BCA = `square`
30° – 60° – 90° त्रिकोणाच्या प्रमेयानुसार,
`square = 1/2 "AC" व square = sqrt3/2 "AC"`.
∴ BC = `1/2 xx square` व AB = `sqrt3/2 xx 14`
BC = 7 व AB = `7sqrt3`.
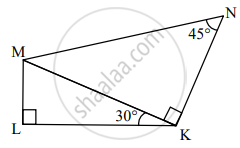
सोबतच्या आकृतीत, LK = `6sqrt2` तर MK, ML, MN काढा.