Advertisements
Advertisements
Question
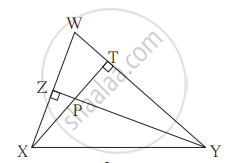
आकृती मध्ये, रेख YZ आणि रेख XT हे ΔWXY चे शिरोलंब बिंदू P मध्ये छेदतात तर सिद्ध करा,
(1) `square`WZPT हा चक्रीय आहे.
(2) बिंदू X, Z, T, Y एकाच वर्तुळावर आहेत.
Solution
पक्ष: रेख YZ ⊥ रेख XW
रेख XT ⊥ रेख WY
साध्य:
(1) `square`WZPT हा चक्रीय आहे.
(2) बिंदू X, Z, T, Y एकाच वर्तुळावर आहेत.
सिद्धता:
(1) रेख YZ ⊥ रेख XW .....[पक्ष]
∴ ∠PZW = 90° ....(i)
रेख XT ⊥ रेख WY .......[पक्ष]
∴ ∠PTW = 90° ......(ii)
∠PZW + ∠PTW = 90° + 90° ....[(i) व (ii) ची बेरीज करून]
∴ ∠PZW + ∠PTW = 180°
∴ `square`WZPT हा चक्रीय चौकोन आहे. .....[चक्रीय चौकोनाच्या प्रमेयाचा व्यत्यास]
(2) ∠XZY = ∠YTX = 90° .....[पक्ष]
∴ रेषा XY वरील बिंदू X व Y हे रेषा XY च्या एकाच बाजूला एकरूप कोन निश्चित करतात.
∴ बिंदू X, Z, T व Y हे एकाच वर्तुळावर आहेत. ....[रेषेचे दोन भिन्न बिंदू, त्या रेषेच्या एकाच बाजूला असणाऱ्या दोन भिन्न बिंदूशी एकरूप कोन निश्चित करत असतील, तर ते चार बिंदू एकाच वर्तुळावर असतात.]
APPEARS IN
RELATED QUESTIONS
कोणताही आयत हा चक्रीय चौकोन असतो हे सिद्ध करा.
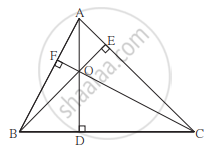
ΔABC मध्ये, रेख AD ⊥ बाजू BC, रेख BE ⊥ बाजू AC, रेख CF ⊥ बाजू AB. बिंदू O हा शिरोलंबसंपात आहे. तर बिंदू O हा ΔDEF चा अंतर्मध्य होतो, हे सिद्ध करा.
चक्रीय `square`MRPN मध्ये, ∠R = (5x - 13)° आणि ∠N = (4x + 4)°, तर ∠R आणि ∠N यांची मापे काढण्यासाठी खालील कृती पूर्ण करा.
उकल:
`square`MRPN हा चक्रीय चौकोन आहे.
चक्रीय चौकोनाचे संमुख कोन परस्परांचे `square` असतात.
∠R + ∠N = `square`
∴ (5x - 13)° + (4x + 4)° = `square`
∴ 9x = 189
∴ x = `square`
∴ ∠R = (5x - 13)° = `square`
∴ ∠N = (4x + 4)° = `square`
