Advertisements
Advertisements
Question
आकृति में, यदि PQR केंद्र O वाले वृत्त की बिंदु Q पर स्पर्श रेखा है, AB रेखा PR के समांतर एक जीवा है तथा ∠BQR = 70° है, तो ∠AQB बराबर ______ है।
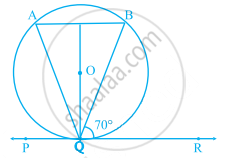
Options
20°
40°
35°
45°
Solution
आकृति में, यदि PQR केंद्र O वाले वृत्त की बिंदु Q पर स्पर्श रेखा है, AB रेखा PR के समांतर एक जीवा है तथा ∠BQR = 70° है, तो ∠AQB बराबर 40° है।
स्पष्टीकरण:
दिया गया है, AB ॥ PR
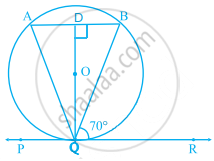
∴ ∠ABQ = ∠BQR = 70° ...[वैकल्पिक कोण]
साथ ही, QD, AB पर लंबवत है और QD, AB को समद्विभाजित करता है।
∆QDA और ∆QDB में,
∠QDA = ∠QDB ...[90° प्रत्येक]
AD = BD
QD = QD ...[सामान्य पक्ष]
∆ADQ ≅ ∆BDQ ...[SAS सर्वांगसमता द्वारा]
⇒ ∠QAD = ∠QBD [CPCT]...(i)
लेकिन ∠QBD = ∠ABQ = 70°
⇒ ∠QAD = 70° ...[(i) से]
अब, ∆ABQ में,
∠A + ∠B + ∠AQB = 180° ...[कोण योग गुण]
⇒ ∠AQB = 180° – (70° + 70°) = 40°
APPEARS IN
RELATED QUESTIONS
आकृति में, यदि ∠AOB = 125° है, तो ∠COD बराबर ______ है।
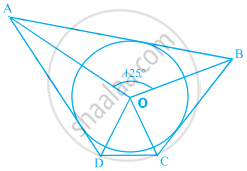
किसी 5 cm त्रिज्या वाले वृत्त के एक व्यास AB के एक सिरे A पर स्पर्श रेखा XAY खींची गई है। XY के समांतर तथा A से 8 cm की दूरी पर, जीवा CD की लंबाई ______ है।
आकृति में, AT केंद्र O वाले वृत्त पर एक स्पर्श रेखा इस प्रकार है कि OT = 4 cm और ∠OTA = 30° है। तब, AT बराबर ______ है।

उपरोक्त प्रश्न 5 में, यदि दोनों वृत्तों की त्रिज्याएँ बराबर हों, तो सिद्ध कीजिए कि AB = CD है।
एक वृत्त की जीवा PQ, बिंदु R पर इस वृत्त की स्पर्श रेखा के समांतर है। सिद्ध कीजिए कि बिंदु R चाप PRQ को समद्विभाजित करता है।
सिद्ध कीजिए कि किसी वृत्त का एक व्यास AB उन सभी जीवाओं को समद्विभाजित करता है, जो बिंदु A से खींची गई वृत्त की स्पर्श रेखा के समांतर हैं।
केंद्रों O और O' वाले तथा क्रमशः त्रिज्याओं 3 cm और 4 cm वाले दो वृत्त परस्पर बिंदुओं P और Q पर इस प्रकार प्रतिच्छेद करते हैं। कि OP और O' P दोनों वृत्तों की स्पर्श रेखाएँ हैं। उभयनिष्ठ जीवा PQ की लंबाई ज्ञात कीजिए।
केंद्र O वाले किसी वृत्त का AB एक व्यास है और AC एक जीवा इस प्रकार है कि ∠BAC = 30° है। C पर वृत्त की स्पर्श रेखा बढ़ाई गई AB को बिंदु D पर प्रतिच्छेद करती है। सिद्ध कीजिए कि BC = BD है।
आकृति में, O त्रिज्या 5 cm वाले वृत्त का केंद्र है, T एक बिंदु इस प्रकार है कि OT = 13 cm है तथा OT वृत्त को E पर प्रतिच्छेद करती है। यदि AB, बिंदु E पर वृत्त की एक स्पर्श रेखा है तो AB की लंबाई ज्ञात कीजिए।
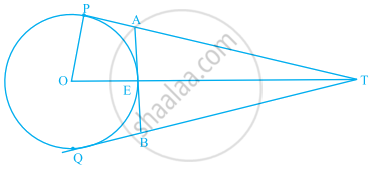
यदि त्रिज्या 9 cm वाले एक वृत्त के अंतर्गत एक समद्विबाहु त्रिभुज ABC खींचा गया है, जिसमें AB = AC = 6 cm है, तो उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
