Question

ΔABC असा काढा, की AB = 8 सेमी, BC = 6 सेमी, ∠B = 90°. रेख BD हा कर्ण AC ला लंब काढा. बिंदू B, D व A मधून जाणारे वर्तुळ काढा. तसेच रेषा BC ही वर्तुळाची स्पर्शिका आहे याचे स्पष्टीकरण द्या.

Answer 1

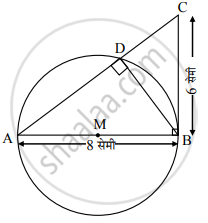
कच्ची आकृती

विश्लेषण:  

रेख BD ⊥ रेख AC

∴ ΔADB हा काटकोन त्रिकोण आहे.

∴ रेख AB हा A, B व D बिंदूंमधून जाणाऱ्या वर्तुळाचा व्यास आहे.

∴ रेख MB ही वर्तुळाची त्रिज्या आहे.

∠MBC हा काटकोन त्रिकोण आहे. ….....[पक्ष]

∴ रेषा BC ही वर्तुळाची स्पर्शिका आहे.

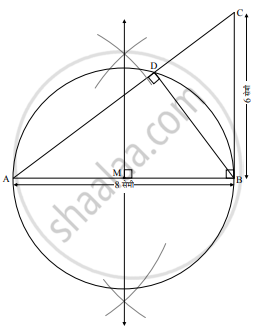
रचनेच्या पायऱ्या: 

1. 8 सेमी लांबीचा रेख AB काढा.
2. 6 सेमी लांबीचा रेख CB अशाप्रकारे काढा, की रेख CB ⊥ रेख AB.
3. रेख AC जोडून ΔABC मिळवा.
4. बिंदू B वरून कर्ण AC ला लंब काढा. या लंबाच्या AC वरील बिंदूला D नाव द्या.
5. रेख AB चा दुभाजक काढा.
6. M हे वर्तुळ व l(MB) ही त्रिज्या घेऊन बिंदू B, D आणि A मधून जाणारे वर्तुळ काढा.