Advertisements
Advertisements
Question
∆ABC with vertices A(–2, 0), B(2, 0) and C(0, 2) is similar to ∆DEF with vertices D(–4, 0), E(4, 0) and F(0, 4).
Options
True
False
Solution
This statement is True.
Explanation:
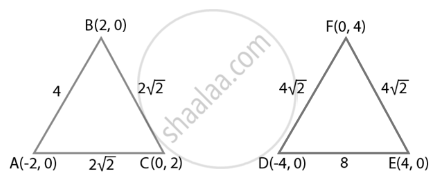
Using distance formula,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
We can find,
AB = `sqrt((2 + 2)^2 + 0) = sqrt(16)` = 4
BC = `sqrt((0 - 2)^2 + (2 - 0)^2) = sqrt(8) = 2sqrt(2)`
CA = `sqrt((-2 - 0)^2 + (0 - 2)^2) = sqrt(8) = 2sqrt(2)`
DE = `sqrt((4 + 4)^2 + 0) = sqrt(64)` = 8
EF = `sqrt((0 - 4)^2 + (4 - 0)^2) = sqrt(32) = 4sqrt(2)`
FD = `sqrt((-4 - 0)^2 + (0 - 4)^2) = sqrt(32) = 4sqrt(2)`
∴ `("AB")/("DE") = ("BC")/("EF") = ("CA")/("FD") = 1/2`
⇒ ΔABC ∼ ΔDEF
Hence, triangle ABC and DEF are similar.
APPEARS IN
RELATED QUESTIONS
If the point P(x, y ) is equidistant from the points A(5, 1) and B (1, 5), prove that x = y.
Find the distance of the following point from the origin :
(6 , 8)
Find the distance between the following point :
(sin θ , cos θ) and (cos θ , - sin θ)
Find the distance of a point (7 , 5) from another point on the x - axis whose abscissa is -5.
Find the distance of a point (12 , 5) from another point on the line x = 0 whose ordinate is 9.
In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
Find the distance between the following pairs of point:
`(sqrt(3)+1,1)` and `(0, sqrt(3))`
A point A is at a distance of `sqrt(10)` unit from the point (4, 3). Find the co-ordinates of point A, if its ordinate is twice its abscissa.
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Find distance between points P(– 5, – 7) and Q(0, 3).
By distance formula,
PQ = `sqrt(square + (y_2 - y_1)^2`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(125)`
= `5sqrt(5)`
