Arrange surds in descending order: 53,49,36 - Mathematics

Arrange surds in descending order:

`root(3)(5), root(9)(4), root(6)(3)`

Sum

L.C.M of 3, 9 and 6 is 18

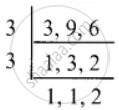
`root(3)(5) = root(3 xx 6)(5^6) = root(18)(15625)`

`root(9)(4) = root(2 xx 9)(4^2) = root(18)(16)`

`root(6)(3) = root(3 xx 6)(3^3) = root(18)(27)`

`root(18)(15625) > root(18)(27) > root(18)(16)`

`root(3)(5) > root(6)(3) > root(9)(4)`

shaalaa.com

Order of a Surd

Is there an error in this question or solution?

Chapter 2: Real Numbers - Exercise 2.6 [Page 68]

Chapter 2 Real Numbers
Exercise 2.6 | Q 4. (i) | Page 68

Arrange surds in descending order:

`root(2)root(3)(5), root(3)root(4)(7), sqrt(sqrt(3)`

Can you get a pure surd when you find the sum of two surds Justify answer with an example

Can you get a pure surd when you find the product of two surds Justify answer with an example.

Can you get a pure surd when you find the quotient of two surds Justify answer with an example

Can you get a rational number when you compute the sum of two surds Justify answer with an example

Can you get a rational number when you compute the difference of two surds Justify answer with an example

Can you get a rational number when you compute the product of two surds Justify answer with an example

Can you get a rational number when you compute the quotient of two surds Justify answer with an example

Find the odd one out of the following.

If `sqrt(80) = "k"sqrt(5)`, then k =