Advertisements
Advertisements
Question
- Assertion (A): The deflecting torque acting on a current-carrying loop is zero when its plane is perpendicular to the direction of the magnetic field.
- Reason (R): The deflecting torque acting on a loop of the magnetic moment `vecm` in a magnetic field `vecB` is given by the dot product of `vecm` and `vecB`.
Options
Both Assertion (A) and Reason (R) are true and (R) is the correct explanation of (A).
Both Assertion (A) and Reason (R) are true and (R) is not the correct explanation of (A).
Assertion (A) is true and Reason (R) is false.
Assertion (A) is false and Reason (R) is also false.
Solution
Assertion (A) is true and Reason (R) is false.
Explanation:
The deflecting torque acting on a current-carrying loop placed in a magnetic field is given by the equation:
`vectau = vecm xx vecB`
Where τ is the deflecting torque, m is the magnetic moment of the loop, and B is the magnetic field. The symbol "x" denotes the vector product.
When the plane of the loop is perpendicular to the direction of the magnetic field, the angle between the magnetic moment vector and the magnetic field vector is 90°.
Both the deflecting torque and the vector product of the two vectors attain their maximum levels in this condition. However, the dot product of the two vectors is zero.
APPEARS IN
RELATED QUESTIONS
A rectangular loop of wire of size 2 cm × 5 cm carries a steady current of 1 A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire.

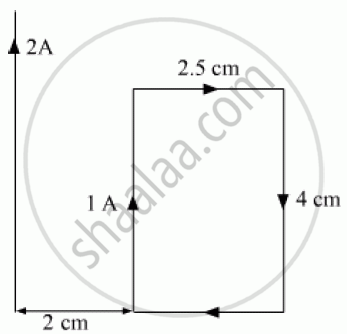
A rectangular loop of wire of size 2.5 cm × 4 cm carries a steady current of 1 A. A straight wire carrying 2 A current is kept near the loop as shown. If the loop and the wire are coplanar, find the (i) torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire.
A rectangular loop of size l × b carrying a steady current I is placed in a uniform magnetic field `vecB`. Prove that the torque `vectau`acting on the loop is give by `vectau =vecm xx vecB,`where `vecm` is the magnetic moment of the loop.
A magnetised needle of magnetic moment 4.8 × 10−2 JT−1 is placed at 30° with the direction of uniform magnetic field of magnitude 3 × 10−2 T. Calculate the torque acting on the needle.
The rectangular wire-frame, shown in figure, has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t = 0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. Find this velocity v0. (c) Show that the velocity at time t is given by
v = v0(1 − e−Ft/mv0).
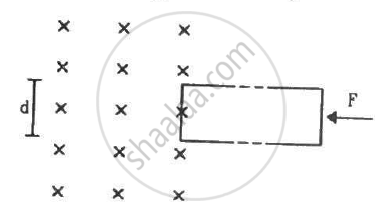
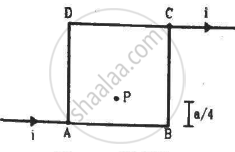
Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
Find the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
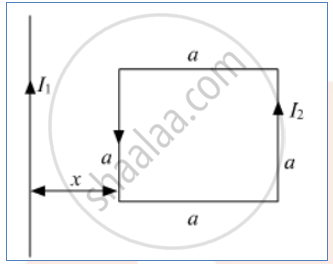
A square loop of side 'a' carrying a current I2 is kept at distance x from an infinitely long straight wire carrying a current I1 as shown in the figure. Obtain the expression for the resultant force acting on the loop.
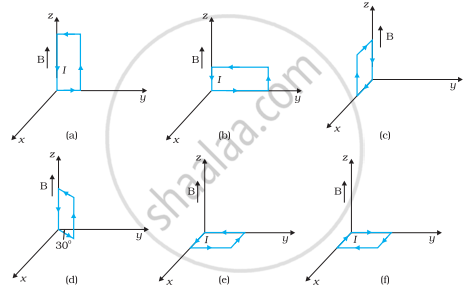
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in fig.? What is the force on each case? Which case corresponds to stable equilibrium?