Advertisements
Advertisements
Question
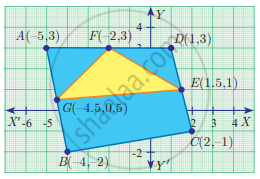
Calculate the area of the figure given below: which is not drawn scale.
Solution
Here we found two geometrical figures, one is a triangle and the other is the trapezium.
Now,
Area of the Triangle = `1/2` x 12 x 25
= 150 sq.cm
Area of Trapezium = `1/2 xx ( 25 + 15 ) xx ( sqrt(26^2 - ( 25 - 15 )^2))`
= 20 x 24
= 480 sq.cm
hence area of the whole figure = 150 + 480 = 630 sq.cm
APPEARS IN
RELATED QUESTIONS
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
How many tiles, each of area 400 cm2, will be needed to pave a footpath which is 2 m wide and surrounds a grass plot 25 m long and 13 m wide?
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio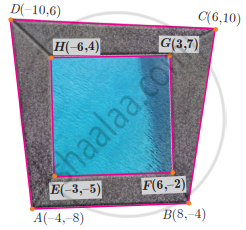
Find the area of quadrilateral BCEG