Advertisements
Advertisements
Question
Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave front traverses through the lens and after refraction focusses on the focal point of the lens, giving the shape of the emergent wave front.
Solution
The new position of the wavefront at any instant (called secondary wave front) is the envelope of the secondary wavelets at that instant.
Incident wave front traversing through the lens and after refraction focusing on the focal point of the lens is shown in the figure below.
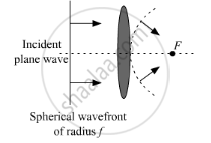
APPEARS IN
RELATED QUESTIONS
Using Huygens's construction of secondary wavelets explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a monochromatic beam of light is incident normally.
What is the shape of the wavefront in the following case?
Light diverging from a point source.
What is the shape of the wavefront in the following case?
The portion of the wavefront of light from a distant star was intercepted by the Earth.
State Huygens’s principle. Show, with the help of a suitable diagram, how this principle is used to obtain the diffraction pattern by a single slit.
Draw a plot of intensity distribution and explain clearly why the secondary maxima becomes weaker with increasing order (n) of the secondary maxima.
Huygens' principle of secondary wavelets may be used to
(a) find the velocity of light in vacuum
(b) explain the particle behaviour of light
(c) find the new position of a wavefront
(d) explain Snell's Law
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
According to Huygen's construction, relation between old and new wavefront is ______.
Is Huygen’s principle valid for longitudinal sound waves?
Two light beams of intensities in the ratio of 9 : 4 are allowed to interfere. The ratio of the intensity of maxima and minima ______.
Represent diagrammatically how the incident planar wavefronts of wavelength λ pass through an aperture of size d, when d is approximately equal to λ.
