Advertisements
Advertisements
Question
Consider a sample of a pure beta-active material.
Options
All the beta particles emitted have the same energy.
The beta particles originally exist inside the nucleus and are ejected at the time of beta decay.
The antineutrino emitted in a beta decay has zero mass and hence zero momentum.
The active nucleus changes to one of its isobars after the beta decay.
Solution
The active nucleus changes to one of its isobars after the beta decay.
In a beta decay, either a neutron is converted to a proton or a proton is converted to a neutron such that the mass number does not change. Also,the number of the nucleons present in the nucleus remains the same. Thus, the active nucleus gets converted to one of its isobars after beta decay.
APPEARS IN
RELATED QUESTIONS
For the `beta^+` (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K−shell, is captured by the nucleus and a neutrino is emitted).
\[\ce{e+ + ^A_Z X -> ^A_{Z - 1}Y + \text{v}}\]
Show that if `beta^+` emission is energetically allowed, electron capture is necessarily allowed but not vice−versa.
Consider the D−T reaction (deuterium−tritium fusion)
\[\ce{^2_1H + ^3_1H -> ^4_2He + n}\]
Calculate the energy released in MeV in this reaction from the data:
`"m"(""_1^2"H")`= 2.014102 u
`"m"(""_1^3"H")`= 3.016049 u
Consider the D−T reaction (deuterium−tritium fusion)
\[\ce{^2_1H + ^3_1H -> ^4_2He}\]
Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.)
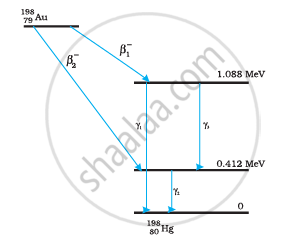
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γdecays in the decay scheme shown in Fig. 13.6. You are given that
m (198Au) = 197.968233 u
m (198Hg) =197.966760 u
Write the basic nuclear process underlying β+ and β– decays.
Write the β-decay of tritium in symbolic form.
Write the basic nuclear process of neutron undergoing β-decay.
Why is the detection of neutrinos found very difficult?
What is the difference between cathode rays and beta rays? When the two are travelling in space, can you make out which is the cathode ray and which is the beta ray?
In beta decay, an electron (or a positron) is emitted by a nucleus. Does the remaining atom get oppositely charged?
Ten grams of 57Co kept in an open container beta-decays with a half-life of 270 days. The weight of the material inside the container after 540 days will be very nearly
A free neutron beta-decays to a proton with a half-life of 14 minutes. (a) What is the decay constant? (b) Find the energy liberated in the process.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Complete the following decay schemes.
(a) `"" _88^226Ra → alpha+`
(b) `""_8^19O → _9^19F+`
(c) `""_13^25Al → ""_12^25Mg+`
