Advertisements
Advertisements
Question
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γdecays in the decay scheme shown in Fig. 13.6. You are given that
m (198Au) = 197.968233 u
m (198Hg) =197.966760 u
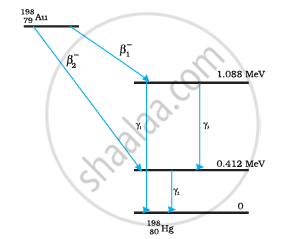
Solution
It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ1-decay is given as:
E1 = 1.088 − 0 = 1.088 MeV
hν1= 1.088 × 1.6 × 10−19 × 106 J
Where,
h = Planck’s constant = 6.6 × 10−34 Js
ν1 = Frequency of radiation radiated by γ1-decay
`therefore "v"_1 = "E"_1/"h"`
`= (1.088 xx 1.6 xx 10^(-19) xx 10^6)/(6.6 xx 10^(-34)) = 2.637 xx 10^20 "Hz"`
It can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ2-decay is given as:
E2 = 0.412 − 0 = 0.412 MeV
hν2= 0.412 × 1.6 × 10−19 × 106 J
Where,
ν2 = Frequency of radiation radiated by γ2-decay
`therefore "v"_2 = "E"_2/"h"`
`= (0.412 xx 1.6 xx 10^(-19) xx 10^6)/(6.6 xx 10^(-34)) = 9.988 xx 10^(19) "Hz"`
It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ3-decay is given as:
E3 = 1.088 − 0.412 = 0.676 MeV
hν3= 0.676 × 10−19 × 106 J
Where,
ν3 = Frequency of radiation radiated by γ3-decay
`therefore "v"_3 = "E"_3/"h"`
`= (0.676 xx 1.6 xx 10^(-19) xx 10^6)/(6.6 xx 10^(-34)) = 1.639 xx 10^20 "Hz"`
Mass of `"m"(""_78^198"Au")`= 197.968233 u
Mass of `"m"(""_80^198 "Hg")`= 197.966760 u
1 u = 931.5 MeV/c2
Energy of the highest level is given as:
E = `["m"(""_78^198 "Au") - "m"(""_80^190 "Hg")]`
`= 197.968233 - 197.966760 = 0.001473 " u"`
`= 0.001473 xx 931.5 = 1.3720955 " MeV"`
β1 decays from the 1.3720995 MeV level to the 1.088 MeV level
∴ Maximum kinetic energy of the β1 particle = 1.3720995 − 1.088
= 0.2840995 MeV
β2 decays from the 1.3720995 MeV level to the 0.412 MeV level
∴ Maximum kinetic energy of the β2 particle = 1.3720995 − 0.412
= 0.9600995 MeV
APPEARS IN
RELATED QUESTIONS
For the `beta^+` (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K−shell, is captured by the nucleus and a neutrino is emitted).
\[\ce{e+ + ^A_Z X -> ^A_{Z - 1}Y + \text{v}}\]
Show that if `beta^+` emission is energetically allowed, electron capture is necessarily allowed but not vice−versa.
Consider the D−T reaction (deuterium−tritium fusion)
\[\ce{^2_1H + ^3_1H -> ^4_2He + n}\]
Calculate the energy released in MeV in this reaction from the data:
`"m"(""_1^2"H")`= 2.014102 u
`"m"(""_1^3"H")`= 3.016049 u
Consider the D−T reaction (deuterium−tritium fusion)
\[\ce{^2_1H + ^3_1H -> ^4_2He}\]
Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.)
Write the β-decay of tritium in symbolic form.
Write the basic nuclear process of neutron undergoing β-decay.
Why is the detection of neutrinos found very difficult?
What is the difference between cathode rays and beta rays? When the two are travelling in space, can you make out which is the cathode ray and which is the beta ray?
In beta decay, an electron (or a positron) is emitted by a nucleus. Does the remaining atom get oppositely charged?
Ten grams of 57Co kept in an open container beta-decays with a half-life of 270 days. The weight of the material inside the container after 540 days will be very nearly
Consider a sample of a pure beta-active material.
A free neutron beta-decays to a proton with a half-life of 14 minutes. (a) What is the decay constant? (b) Find the energy liberated in the process.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Complete the following decay schemes.
(a) `"" _88^226Ra → alpha+`
(b) `""_8^19O → _9^19F+`
(c) `""_13^25Al → ""_12^25Mg+`
