Advertisements
Advertisements
Question
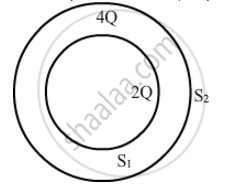
Consider two hollow concentric spheres, S1 and S2, enclosing charges 2Q and 4Q respectively as shown in the figure. (i) Find out the ratio of the electric flux through them. (ii) How will the electric flux through the sphere S1 change if a medium of dielectric constant 'εr' is introduced in the space inside S1 in place of air ? Deduce the necessary expression
Solution
(i) Charge enclosed by sphere S1 = 2Q
By Gauss law, electric flux through sphere S1 is
`phi_1=(2Q)/in_0`
Charge enclosed by sphere S2 = 2Q+4Q=6Q
`:.phi_2=(6Q)/in_0`
The ratio of the electric flux is
`phi_1/phi_2=((2Q)/in_0)/((6Q)/in_0)=2/6=1/3`
(ii) For sphere S1, the electric flux is
`phi'=(2q)/in_r`
`:.(phi')/phi_1=in_0/in_r`
`=>phi'=phi_1.in_0/in_r`
∵ εr > ε0
`:.phi'
Therefore, the electric flux through the sphere S1 decreases with the introduction of the dielectric inside it.
APPEARS IN
RELATED QUESTIONS
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 103 N m2/C.
- What is the net charge inside the box?
- If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
If the flux of the electric field through a closed surface is zero,
(a) the electric field must be zero everywhere on the surface
(b) the electric field may be zero everywhere on the surface
(c) the charge inside the surface must be zero
(d) the charge in the vicinity of the surface must be zero
A uniform electric field of intensity 400 N/C, exists in a certain region. How much flux will cross a given area of 10 cm2 in this region, if the area vector is inclined at 60° to the direction of the field?
An electric charge q is placed at the centre of a cube of side a. The electric flux on one of its faces will be ______.
Total electric flux coming out of a unit positive charge kept in air is ______.
An electric charge q is placed at the center of a cube of side ℓ. The electric flux on one of its faces will be ______.
