Advertisements
Advertisements
Question
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 103 N m2/C.
- What is the net charge inside the box?
- If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Solution
- Φ = 8 × 103 N m2 C-1
or `q/ε_0 = 8 xx 10^3` N m2 C-1
or q = 8 × 103ε0
= 8 × 103 × 8.85 × 10-12
or q = 7.08 × 10-8 C - As Φ = 0
or `q_"net"/ε_0 = 0 or q_"net" = 0`
Even though a closed surface may have internal charges, the net charge it contains is zero.
APPEARS IN
RELATED QUESTIONS
Define electric flux.
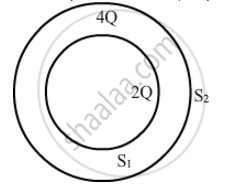
Consider two hollow concentric spheres, S1 and S2, enclosing charges 2Q and 4Q respectively as shown in the figure. (i) Find out the ratio of the electric flux through them. (ii) How will the electric flux through the sphere S1 change if a medium of dielectric constant 'εr' is introduced in the space inside S1 in place of air ? Deduce the necessary expression
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
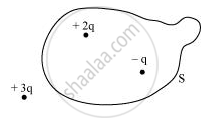
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
A charge q is placed at the centre of the open end of a cylindrical vessel (see the figure). The flux of the electric field through the surface of the vessel is ____________ .

Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be _____________ .
The electric field in a region is given by `vec"E"` = 5 `hatk`N/C. Calculate the electric flux Through a square of side 10.0 cm in the following cases
- The square is along the XY plane
- The square is along XZ plane
- The normal to the square makes an angle of 45° with the Z axis.
A uniform electric field of intensity 400 N/C, exists in a certain region. How much flux will cross a given area of 10 cm2 in this region, if the area vector is inclined at 60° to the direction of the field?
A charged particle q is placed at the centre O of cube of length L (A B C D E F G H). Another same charge q is placed at a distance L from O. Then the electric flux through ABCD is ______.
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The total flux for the surface of the cylinder is given by ______.
The electric field intensity due to an infinite cylinder of radius R and having charge q per unit length at a distance rir r(r > R) from its axis is ______.
The electric field in a region is given by `bar"E" = 4hat"i" + 10hat"j"` N/C. The flux of this field through a square of 10 cm on a side whose plane is parallel to the XZ plane.
In a region of space having a uniform electric field E, a hemispherical bowl of radius r is placed. The electric flux Φ through the bowl is:
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
