Advertisements
Advertisements
Question
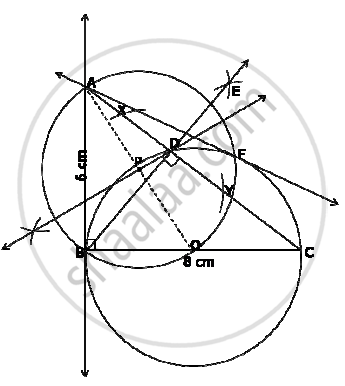
Construct a right triangle ABC with AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD, the perpendicular from B on AC. Draw the circle through B, C and D and construct the tangents from A to this circle.
Solution
Steps of construction:
1) Construct the triangle as per given measurements.
2) Take any arbitrary radius and draw two arcs of circle from point B on AC, intersecting AC at X and Y.
3) Taking X and Y as centres, draw two arcs of circles to intersect each other at point E. Join B and E. BE is the perpendicular from B on AC.
4) DBDC is a right angled. Hence, BC the hypotenuse will form the diameter of the circle passing through the vertices of ΔBDC.
5) BC = 8 cm OC = 4 cm. draw a circle of radius equal 4 cm, passing through B, D and C.
6) Join O and A. Obtain the mid-point P of segment OA by drawing perpendicular bisector to OA.
7) Draw a circle with centre P and radius AP.
8) Let B and F be the points of intersection of these two circles. Hence, AB and AF are the required tangents.
APPEARS IN
RELATED QUESTIONS
Draw a triangle ABC with BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are `3/4` of the corresponding sides of the ∆ABC.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `7/5`of the corresponding sides of the first triangle.
Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ΔABC
Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠AB = 60° . Construct another ΔAB'C ' similar to ΔABC with base AB’ = 8 cm.
Construct a ΔABC in which BC = 8 cm, ∠B = 45° and ∠C = 60° . Construct another triangle similar to ΔABC such that its sides are `3/5`of the corresponding sides of ΔABC .
To construct a triangle similar to ΔABC in which BC = 4.5 cm, ∠B = 45° and ∠C =60° , using a scale factor of `3/7`, BC will be divided in the ratio
(a) 3 : 4 (b) 4 : 7 (c) 3 : 10 (d) 3 : 7
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3cm. Then, construct another triangle whose sides are `5/3`times the corresponding sides of the given triangle.
Draw a triangle ABC with BC = 7 cm, ∠ B = 45° and ∠C = 60°. Then construct another triangle, whose sides are `3/5` times the corresponding sides of ΔABC.
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
Construct a triangle PQR with sides QR = 7 cm, PQ = 6 cm and \[\angle\]PQR = 60º. Then construct another triangle whose sides are \[\frac{3}{5}\] of the corresponiding sides of ∆PQR.
