Advertisements
Advertisements
Question
Define the capacitance of a capacitor. Obtain the expression for the capacitance of a parallel plate capacitor in vacuum in terms of plate area A and separation d between the plates.
Solution
The capacitance of a capacitor is the amount of charge which creates unit potential difference between collecting plate and condensing plate after giving charge on the collecting plate.
Parallel Plate Capacitor
-
A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance.

-
Let A be the area of each plate and d the separation between them. The two plates have charges Q and −Q.
-
Surface charge density of plate 1, σ = Q/A, and that of plate 2 is σ.
-
Electric field in different regions:
Outer region I,
`E = σ/(2ε_0) - σ/(2ε_0 ) = 0`
In the inner region between plates 1 and 2, the electric fields due to the two charged plates add up. So,
\[E = \frac{\sigma}{2 \epsilon_0} + \frac{\sigma}{2 \epsilon_0} = \frac{\sigma}{\epsilon_0} = \frac{Q}{\epsilon_0 A}\]
E=σ2ε0+σ2ε0=σε0=Qε0
-
The direction of electric field is from the positive to the negative plate.
-
For uniform electric field, potential difference is simply the electric field multiplied by the distance between the plates, i.e.
`V=Ed = 1/c (Qd)/A`
Capacitance C of the parallel plate capacitor in vacuum is
`C = Q/V =(ε_0A)/d `
APPEARS IN
RELATED QUESTIONS
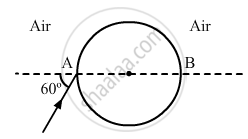
A ray of light falls on a transparent sphere with centre C as shown in the figure. The ray emerges from the sphere parallel to the line AB. Find the angle of refraction at A if the refractive index of the material of the sphere is \[\sqrt{3}\].
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10−3m2 and the separation between the plates is 3 mm.
- Calculate the capacitance of the capacitor.
- If this capacitor is connected to 100 V supply, what would be the charge on each plate?
- How would charge on the plates be affected, if a 3 mm thick mica sheet of k = 6 is inserted between the plates while the voltage supply remains connected?
A parallel-plate capacitor is charged to a potential difference V by a dc source. The capacitor is then disconnected from the source. If the distance between the plates is doubled, state with reason how the following change:
(i) electric field between the plates
(ii) capacitance, and
(iii) energy stored in the capacitor
A parallel-plate capacitor with plate area 20 cm2 and plate separation 1.0 mm is connected to a battery. The resistance of the circuit is 10 kΩ. Find the time constant of the circuit.
A parallel-plate capacitor of plate area 40 cm2 and separation between the plates 0.10 mm, is connected to a battery of emf 2.0 V through a 16 Ω resistor. Find the electric field in the capacitor 10 ns after the connections are made.
A parallel plate air condenser has a capacity of 20µF. What will be a new capacity if:
1) the distance between the two plates is doubled?
2) a marble slab of dielectric constant 8 is introduced between the two plates?
Solve the following question.
A parallel plate capacitor is charged by a battery to a potential difference V. It is disconnected from the battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
In a parallel plate capacitor, the capacity increases if ______.
A parallel plate capacitor is connected to a battery as shown in figure. Consider two situations:
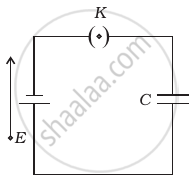
- Key K is kept closed and plates of capacitors are moved apart using insulating handle.
- Key K is opened and plates of capacitors are moved apart using insulating handle.
Choose the correct option(s).
- In A: Q remains same but C changes.
- In B: V remains same but C changes.
- In A: V remains same and hence Q changes.
- In B: Q remains same and hence V changes.
Two charges – q each are separated by distance 2d. A third charge + q is kept at mid point O. Find potential energy of + q as a function of small distance x from O due to – q charges. Sketch P.E. v/s x and convince yourself that the charge at O is in an unstable equilibrium.
